Визначення оптичних констант плівок на прозорій підкладці
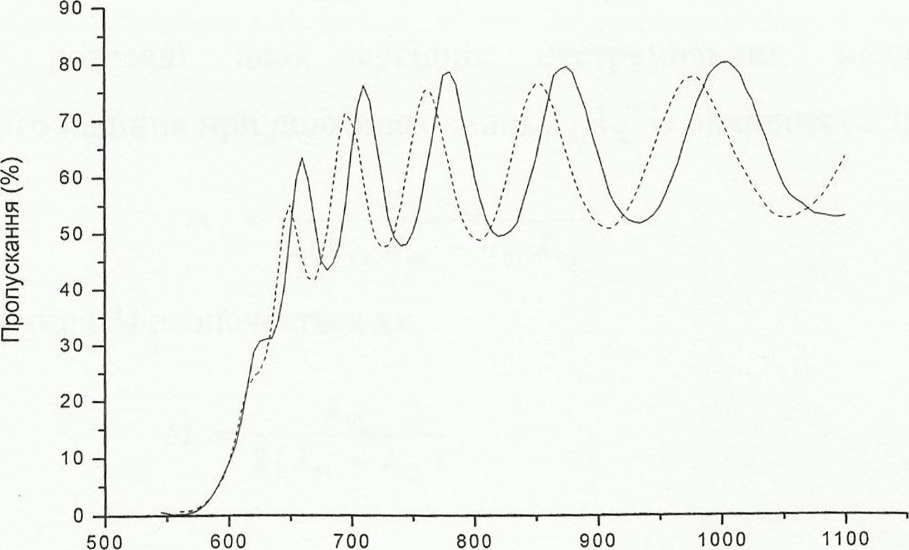
Тонкі плівки товщиною порядка 1 мкм широко використовуються в оптоелектроніці [5-8]. Товщина цих плівок дуже важливий параметр і її можна визначити без розрушення об'єкта дослідження по оптичному спектру пропускання. Спектр також дає можливість визначити значення показника заломлення п(λ). Теорія оптичного пропускання тонких плівок на прозорих підкладках досліджувалась багатьма дослідниками [9-11]. Були запропоновані прості прямі операції для випадку k2˂˂п2, (k –уявна частина показника). Це включає в себе побудову неперервних огинаючих Ттах і Ттіп навколо максимумів і мінімумів інтерференційних смуг [10]. Якщо коефіцієнт заломлення підкладки s значення n записується у вигляді [11,12].
де
Рівняння (2.1) вимагає, щоб Ттах і Ттіп вимірювалося з точністю більше 0,5%, щоб n було обчислено з точністю 1% [12]. Із теорії нормальної дисперсії слідує, що п(λ) можна точно описати трьома постійними х, а і b в області k2˂˂п2за допомогою рівняння
В недисперсній довгохвильовій області значення n тоді буде
Розглянемо випадок, коли n плівки більше за показник заломлення підкладки, а тоді m має цілі значення для максимумів і півцілі для мінімумів. Тому задача зводиться до визначення п'яти постійних: m, d,x,a,і b із спектрів пропускання. Із рівнянь (2.2) і (2.3) можна визначити тільки т і x, а також n0d, і потрібно знайти друге експериментальне рівняння. Це можна зробити, якщо дістати ще один спектр пропускання при куті падіння i >0. Рівняння для експериментальних значень інтерференції тоді прийме вигляд [12]:
де r - це кут заломлення у плівці. П’ять постійних можна тепер визначити із рівнянь (2.2)-(2.4) різними методами, якщо є хоча б 3 експериментальних значення.
Довжина хвилі, нм
Рис. 2.1. Спектр пропускання плівки a-Si:Н товщиною 1мкм. на скляній підкладці для нормального падіння (суцільна лінія) і кута падіння 30°(пунктирна лінія) [12].
|

 (2.1)
(2.1)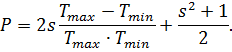
 (2.2)
(2.2)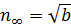 . Для нормального падіння світла на плівку товщиною d, довжини хвиль крайніх значень, дані в уже відомому рівнянні
. Для нормального падіння світла на плівку товщиною d, довжини хвиль крайніх значень, дані в уже відомому рівнянні (2.3)
(2.3) (2.4)
(2.4)