Експериментальна установка і методика дослідження оптичних констант плівок.
Не дивлячись на те, що вже більше ніж за 50 років із часу відкриття ХСН їх властивості досить добре вивчені, навіть останнім часом не зникає інтерес як до їх технології одержання[13], так і подальше дослідження їх фізико-хімічних, оптичних властивостей та застосування[14-20]. Інтерес до використання різних багатокомпонентних стекол і плівок на їх основі в оптиці підкреслює важливість вивчення оптичних властивостей цих матеріалів. Халькогенідні стекла відрізняються від інших прозорих твердих тіл своїми оптичними константами на діаграмі Аббе і вони мають відносне велике значеня показника заломлення n і низький коефіцієнт дисперсії. Халькогенідні тонкоплівкові шари, що використовуються у наших дослідженнях, відносяться до сімейства системи As-Se. Для вимірювання коефіцієнту пропускання використовувався спектрофотометр СФ-46. В основу роботи спектрофотометра СФ-46 покладений принцип вимірювання відношення інтенсивностей двох світлових потоків: потоку, що пройшов через досліджуваний зразок, і потоку, падаючого на досліджуваний зразок (або що пройшов через контрольний зразок). Структурна схема спектрофотометра представлена на рис. 2.3.
Рис. 2.3. Структурна схема спектрофотометра СФ-46 [21].
Світловий пучок з освітлювача потрапляє в монохроматор через вхідну щілину і розкладається дифракційною граткою в спектр. У монохроматичний потік випромінювання, що поступає з вихідної щілини в кюветне відділення, по черзі вводяться контрольний і досліджуваний зразки. Випромінювання, що пройшло через зразок, потрапляє на катод фотоелемента в приймально-підсилювальному блоці. Електричний струм, що проходить через резистор, який включений в анодний ланцюг фотоелемента, створює на резисторі падіння напруги, пропорційне потоку випромінювання, падаючому на фотокатод. Підсилювач постійного струму з коефіцієнтом підсилення, близьким до одиниці, забезпечує передачу сигналів на вхід мікропроцесорної системи (далі – МПС). МПС по команді оператора по черзі вимірює і запам’ятовує напруги UT, U0 і U, пропорційні темновому струму фотоелемента, потоку, що пройшов через контрольний зразок, і потоку, що пройшов через досліджуваний зразок. Після вимірювання МПС розраховує коефіцієнт пропускання Т досліджуваного зразка по формулі:
Значення виміряної величини висвічується на цифровому фотометричному табло [21]. Оптична схема спектрофотометра представлена на рис. 2.4. Випромінювання від джерела 1 або 1' падає на дзеркальний конденсатор 2, який направляє його на плоске поворотне дзеркало 3 і дає зображення джерела випромінювання в площині лінзи 4, розташованої поблизу вхідної щілини 5 монохроматора. Монохроматор побудований по вертикальній автоколімаційній схемі. Випромінювання, що пройшло через вхідну щілину, падає на увігнуту дифракційну гратку 6 із змінним кроком і криволінійним штрихом. Гратки виготовляються на сферичній поверхні, тому, крім диспергуючих властивостей, вона володіє властивістю фокусувати спектр. Застосування змінного кроку і криволінійного штриха значно зменшує абераційні спотворення увігнутих дифракційних граток і дозволяє одержати високу якість спектру у всьому робочому спектральному діапазоні. Дифрагований пучок фокусується в площині вихідної щілини 7 монохроматора, розташованої над вхідною щілиною 5. Сканування здійснюється поворотом дифракційної гратки, при цьому монохроматичне випромінювання різних довжин хвиль проходить через вихідну щілину 7, лінзу 8, контрольний або вимірювальний зразок, лінзу 9 з допомогою поворотного дзеркала 10 потрапляє на світлочутливий шар фотоелемента 11 або 12.

Рис. 2.4. Оптична схема спектрофотометра СФ-46 [21].
2.3. Експериментальні результати та методика їх обрахунку
Край поглинання склоподібних матеріалів характеризується наявністю трьох характерних ділянок на енергетичній залежності α=f(hv) (рис.2.5.). Ділянка А характеризується поглинанням при малих значеннях α. Це — довгохвилева частина оптичного “хвоста”, що залежить від чистоти вихідних компонент і досконалості структури. Для неї характерна експоненціальна залежність[22]. α ≈ exp(Гt · hv), (2.5) де Гt — небагато менша ніж Г. Автори роботи [23, 24] вважають, що ділянка слабого поглинання пов’язана з флуктуаціями потенціалу, які можуть виникати у зв’язку з втратами дальнього порядку, наявністю дефектів або домішок. Ділянка В (рис.2.5) характеризується експоненціальною залежністю:
де На ділянці С (рис.2.5) hν ·α (hν) ≈ const [hν – Eg (T)]2 (2.27) В цьому випадку із залежності
Перехід від квадратично-кореневої залежності до лінійної спостерігається і в склоподібній системі As-S при надлишку халькогена відносно As2S3 і для складу As0,43Se0,57[26]. З іншої сторони, залишається неясним, чому співвідношення (2.27) так добре виконується для аморфного As2S3 і не виконується для кристалічного As2S3 [23]. Наукова література містинь великий об’єм інформації щодо краю Урбаха у некристалічних напівпровідниках, зокрема у склах системи As-Se [23,26,27,28]. Область поглинання вищеурбахівського краю досліджено значно менше, хоч емпіричний закон Тауца [22] можна вважати майже настільки ж універсальним для аморфних матеріалів. У більшості випадків, зокрема, нахил краю поглинання у представленні Тауца ігнорується, не зважаючи на те, що окремі параметри, які можна визначити на основі згаданих представлень дають можливість розрахувати абсолютне значення оптичного поглинання при різних енергіях [26]. Насамперед необхідно зауважити, що для переважної більшості аморфних матеріалів, характерним є хороше узгодження
де
Рис.2.5.Типова залежність краю поглинання в склоподібних напівпровідниках [22,23]. З метою перевірки виконання закону Тауца для плівок розрізу AsXSe1-X були проведені дослідження спектрів пропускання цих матеріалів. Коефіцієнт поглинання визначили за формулою:
де, n1 - показник заломлення плівки, n2 - показник заломлення підкладки, Т - пропускання системи плівка-підкладка (у відносних одиницях), d - товщина плівки. За допомогою спектрофотометра, змінюючи довжину хвилі в межах від 450 до 1100 нм, з кроком 5 нм, вимірювали пропускання досліджуваних зразків при нормальному падінні випромінювання. Отримані результати заносили в обчислювальну машину і будували графіки Т=f(λ) для кожного зразка (рис. 2.6). Для зручності приведено графік Т=f(λ) лише одного зразка. Рис. 2.6. Спектр пропускання плівки As0,64Se0.36 на скляній підкладці для нормального падіння. Результати вимірювань α=f(hv),проведених при кімнатній температурі, представлені на рис.2.7. Одержані результати добре узгоджуються з відповідними дослідженнями [26], де приведено результати вимірювань α=f(hv) для аморфних плівок AsXSe1-X при Х=0
де, c1 - константа, Е1 - екстрапольоване значення оптичної щілини. Збільшення концентрації миш’яку в кількості > 2 ат. % спричиняє чітко виражений перехід від “аномальної” лінійної залежності до залежності, що описується рівнянням (2.29).
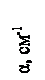
Рис.2.7. Залежність коефіцієнта поглинання від енергії падаючого світла тонкоплівкових шарів розрізу AsXSe1-X. На рис. 2.8 - 2.13 приведено залежності
Рис.2.8.Залежність
Рис.2.9. Залежність
Рис.2.10. Залежність
Рис.2.11. Залежність
Рис.2.12.Залежність
Рис.2.13.Залежність Порівняння літературних даних [26] з нашими вимірюваннями концентраційної залежності Еτ показує, що оптична зона зменшується практично лінійно із збільшенням вмісту миш’яку (рис.2.14) до значень ̴ 40 ат.% As і має мінімум в області 42 ат.% As. Необхідно також зауважити на наявність певної немонотонності Еτ при 4÷6 ат.% As [26, 27]. Схожа композиційна залежність Еτ притаманна і некристалічним зразкам системи Sb-Se з тією різницею, що для останньої подібна особливість спостерігається в інтервалі складів, що містять 2÷3 ат.% Sb [26].

Рис.2.14.Концентраційна залежність ширини забороненої зони системи AsXSe1-X
Оптична щілина Еτ та споріднені з нею інші фізичні параметри визначаються, головним чином, ближнім порядком. В некристалічних халькогенідах AsXSe1-X зона провідності формується антизв’язуючими станами, валентна зона своїм походженням зобов’язана l-p- станами. Для досліджуваних матеріалів зона провідності зростає з ростом Х. Скоріш за все це наслідок ефектів ближнього порядку, які супроводжуються зменшенням атомного об’єму. Враховуючи той факт, що енергія зв’язку As-As, As-Se, і Se-Se (2.07, 2.26, 2.14 еВ відповідно) відрізняються відносно мало, варіацію Еτ із складом, спостережувану нами в зразках системи As-Se, пояснити виключно зміною енергії ковалентних зв’язків досить проблематично. Саме тому, враховуючи одержані експериментальні результати та на основі порівняння з даними інших авторів, концентраційну залежність оптичної щілини можна інтерпретувати наступним чином. В області відносно незначних концентрацій As (0÷3 ат.%) значення Еτ змінюється головним чином, за рахунок зміни ближнього порядку. В інтервалі 0.04<X<0.10 помітне зменшення оптичної щілини відображає зменшення відстані між ланцюжками, а в області концентрації Х=0.40 та Х=0.50 особливості залежностей Еτ від концентрації миш’яку можна пояснити наявністю стехіометричних сполук складу As2Se3 та As4Se4. Таким чином, результати дослідження краю власного поглинання тонкошарових структур AsXSe1-X відтворює концентраційну залежність фото фізичних та фізико-хімічних властивостей у залежності від вмісту миш’яку[26]. Причиною такої поведінки можуть бути певні зміни локальної структури із складом, які спостерігаються на концентраційних залежностях (рис.2.14.)
|


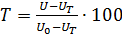 (2.24)
(2.24)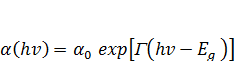 (2.26)
(2.26) - енергія фотона;
- енергія фотона;  ,
, 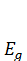 - константи, величини які обумовлені властивостями конкретного матеріалу (Еg - ширина забороненої зони); Г - характеризує нахил краю поглинання. Ця ділянка обумовлена переходами між локалізованими станами в псевдозабороненій зоні, або, що більш ймовірно, між локалізованими і нелокалізованими станами в зонах[22-24].
- константи, величини які обумовлені властивостями конкретного матеріалу (Еg - ширина забороненої зони); Г - характеризує нахил краю поглинання. Ця ділянка обумовлена переходами між локалізованими станами в псевдозабороненій зоні, або, що більш ймовірно, між локалізованими і нелокалізованими станами в зонах[22-24].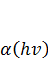 змінюється за законом:
змінюється за законом: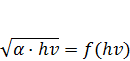 шляхом екстраполяції можна визначити ширину забороненої зони для склоподібних матеріалів. Можливо, таку закономірність слід очікувати в області переходу між нелокалізованими станами, густина яких може бути близькою до критичної. Співставлення експериментальних залежностей
шляхом екстраполяції можна визначити ширину забороненої зони для склоподібних матеріалів. Можливо, таку закономірність слід очікувати в області переходу між нелокалізованими станами, густина яких може бути близькою до критичної. Співставлення експериментальних залежностей 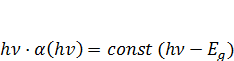 (2.28)
(2.28) , (2.29)
, (2.29) - зона Тауца, c - const, що відображає на скільки різко зростає поглинання з енергією.
- зона Тауца, c - const, що відображає на скільки різко зростає поглинання з енергією.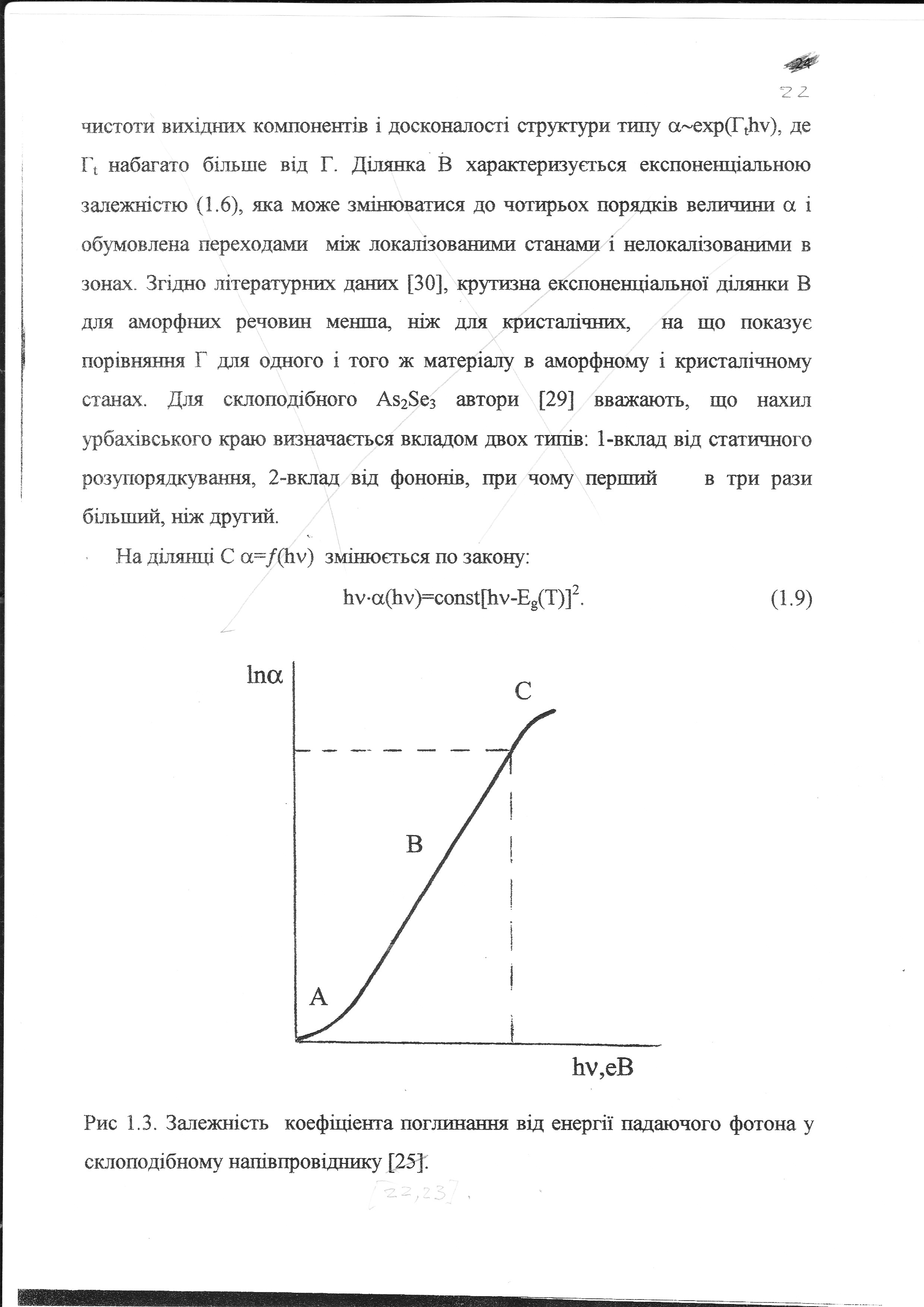
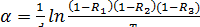 , (2.30)
, (2.30) ;
; 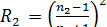 ;
; 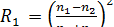 .
. 0.15. Показано, що починаючи з Х=0.02 край поглинання описується рівнянням (2.29), а для 0<х<0.02 в широкому інтервалі енергій падаючих фотонів є лінійна залежність[26]:
0.15. Показано, що починаючи з Х=0.02 край поглинання описується рівнянням (2.29), а для 0<х<0.02 в широкому інтервалі енергій падаючих фотонів є лінійна залежність[26]: , (2.31)
, (2.31)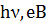
 та
та  по яким можна буде зробити висновки, який закон краще справджується для досліджуваних матеріалів. Аналіз експериментальних результатів показує, що для тонкоплівкових шарів AsXSe1-X області концентрації Х=0.18
по яким можна буде зробити висновки, який закон краще справджується для досліджуваних матеріалів. Аналіз експериментальних результатів показує, що для тонкоплівкових шарів AsXSe1-X області концентрації Х=0.18  0.64, виконується закон Тауца. При цьому, нахил кривих Тауца зменшується із збільшенням концентрації миш’яку (0.18<Х<0.64). Необхідно додати, що верхня межа енергії фотона, до якої виконується згаданий закон, зростає із вмістом миш’яку.
0.64, виконується закон Тауца. При цьому, нахил кривих Тауца зменшується із збільшенням концентрації миш’яку (0.18<Х<0.64). Необхідно додати, що верхня межа енергії фотона, до якої виконується згаданий закон, зростає із вмістом миш’яку.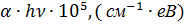
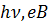
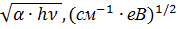
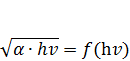 (1) і
(1) і  (2), зразка As0,18Se0,82.
(2), зразка As0,18Se0,82.
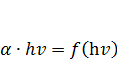 (2), зразка As0,43Se0,57.
(2), зразка As0,43Se0,57.
 (1) і
(1) і 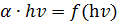 (2), зразка As0,46Se0,54.
(2), зразка As0,46Se0,54. (2), зразка As0,47Se0,53.
(2), зразка As0,47Se0,53.


