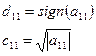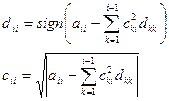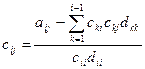Среди уравнений выбирают уравнение, содержащее наибольший по абсолютной величине коэффициент (главный элемент).
Затем уравнение делят на этот главный элемент и из остальных уравнений системы исключают неизвестные, определяемые этим главным элементом.
Далее, оставляя неизменным выбранное уравнение с главным элементом, из остальных уравнений системы выбирают новый главный элемент. Потом это уравнение с новым главным элементом делят на новый главный элемент и исключает неизвестное или определяемое из остальных уравнений системы.
Для удобства главный элемент помещают в левый верхний угол, переставляя строки и столбцы системы уравнений.
В результате преобразований приходим к единичной матрице.
Здесь переставляются уравнения, что приводит к изменению порядка исключенных неизвестных, и во многих случаях уменьшают погрешности, связанные с округлениями.
§16. Метод квадратного корня.
Метод квадратного корня – точный метод решения систем уравнений и он применяется для решения систем уравнений, если матрица А – симметричная, т.е. 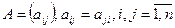 .
.
 ,
,
где С – верхняя треугольная матрица;
 – транспонированная,
– транспонированная,  ;
;
D – диагональная,  .
.
Подставим матрицу А в систему (1) Ах=b.
 (2)
(2)
Тогда
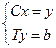 (3)
(3)
Выразим элементы матрицы С через элементы исходной матрицы А.
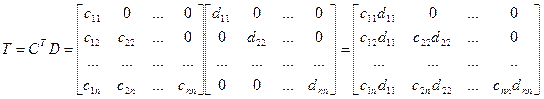 ,
,
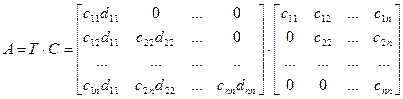 ,
,
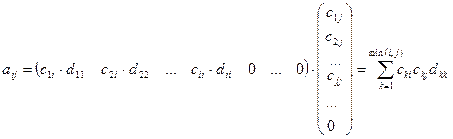 (*)
(*)
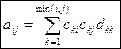 (4)
(4)
Из (4) будем получать выражения  через
через  :
:
Пусть 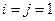 , тогда
, тогда


Пусть 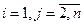 , тогда
, тогда
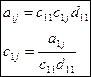
Пусть  , тогда
, тогда


Из формулы (*) получаем:

 ,
, 
Получили формулы:
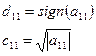

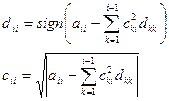
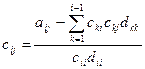
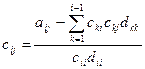 ,
, 

ЛИТЕРАТУРА
1. А.А.Самарский, А.В.Гулин. Численные методы. Москва «Наука», 1989.
- Бахвалов Н. С. Численные методы/ Жидков Н. П., Кобельков Г. М.; МГУ им М. В. Ломоносова. - М.: БИНОМ. Лаборатория знаний, 2006. - 636 с. - ISBN 5-94774-396-5: 372-20, н-1, ч/з-2, общ.8-1, уч-20(1- к ЭВМ); (24:25).
- Киреев В. И. Численные методы в примерах и задачах/ Пантелеев А. В.; М.: Высш. шк., 2008. - 480 с. - ISBN 978-5-06-004763-9: 661-10.(уч-20); (20:25).
- Мудров А. Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль/ Томск: МП"РАСКО", 1991. - 272 с. - ISBN 5-256-00602-9: 11р.20к. н-1; (1:25).
- Калиткин Н. Н. Численные методы/ Под ред. А. А. Самарского. - М.: Наука, 1978. - 512 с. - 1 р. 30 к. КУКП-3, н-4, уч-99, ч/з-3. (110:25)
- Никитенко А. Г. Информатика и компьютерное моделирование в электроаппаратостроении/ Левченко И. И., Гринченков В. П., и др.; М.: Высш. шк., 1999. - 375 с. - ISBN 5-85216-107-1: 98р. с/к-7,н-4,ч/з-4,общ8-2,уч-4.УДК [621.313.002:681.3 + 681.3.01:621.313.002 + 681.322-181.4.001.57:621.313.002 + 681.3.06:800.92; (21:25)
- Ульянов С. А. Электромагнитные переходные процессы в электрических системах/ М.: Энергия, 1970. - 517 с. - 1-17. н-2, общ.8-2, уч-95, ч/з-1; (100:25).
- Кингсли-Хьюджес Э. C# 2005: справочник программиста, пер. с англ./ Кингсли-Хьюджес К.; М., СПб., Киев: Диалектика, 2007. - 368 с. - ISBN 978-5-8459-1288-6: 197-01, 226-67. н-2, ч/з-2; (4:25).
- Меженный О. А. Microsoft Office 2007/ М., СПб., Киев: Диалектика, 2008. - 384 с. - ISBN 978-5-8459-1291-6: 98-01, 109-79. н-2, ч/з-2; (4:25).
- Алямовский А.А. Инженерные расчеты в SolidWorks Simulation/ М.: ДМК Пресс, 2010. - 464 с. - ISBN 978-5-94074-586-0: 405-53. н-2; (2:25).

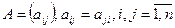 .
. ,
, – транспонированная,
– транспонированная,  ;
; .
. (2)
(2)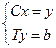 (3)
(3)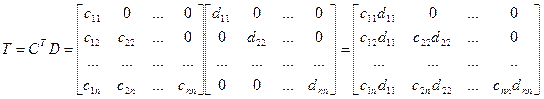 ,
,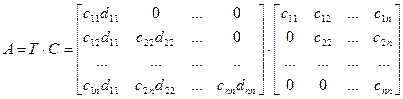 ,
,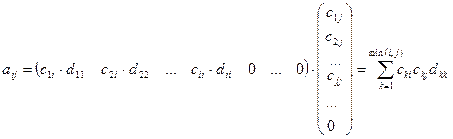 (*)
(*)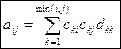 (4)
(4) через
через  :
: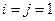 , тогда
, тогда

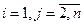 , тогда
, тогда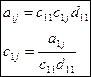
 , тогда
, тогда


 ,
,