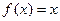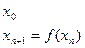Дихотомия (метод деления отрезка пополам).
1. Пусть
2. Рассмотрим Если нужно найти корень с точностью до Дихотомия проста и очень надежна: к простому корню она сходится всегда для любой непрерывной функции в том числе и недифференцируемой, при этом она устойчива к ошибкам округления. Скорость сходимости метода дихотомии не велика, т.е. за одну итерацию точность увеличивается вдвое. Недостатки: прежде чем применить, необходимо найти отрезок, на концах которого функция принимает значения разных знаков. Если на этом отрезке несколько корней, то неизвестно к какому из них сходится дихотомия. Метод не применим к корням четной кратности. Метод применим к корням нечетной кратности, но хуже устойчив к ошибкам округления. Метод не применим к системам уравнений.
§12. Метод простой итерации для решения алгебраических и трансцендентных уравнений. ТЕОРЕМА 1. (Принцип Банаха сжимающихся отображений). Пусть R – полное метрическое пространство. Если
План доказательства. 1.
q – коэффициент сжатия
2. Т.к. R – полное метрическое пространство, то в нем всякая фундаментальная последовательность сходится.
3. ЧТД.
Метод Если в (*)
Метод простой итерации имеет линейную скорость сходимости. Пусть Необходимо привести к виду
Условие сходимости для данного метода:
|

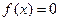
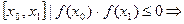 существует хотя бы один корень на
существует хотя бы один корень на 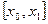 ;
;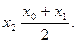
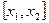 . Из этих двух выберем тот, на концах которого функция
. Из этих двух выберем тот, на концах которого функция 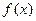 принимает значения разных знаков и поделим его пополам и т.д.
принимает значения разных знаков и поделим его пополам и т.д.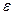 , то мы продолжаем делить отрезок до тех пор, пока длина отрезка не станет меньше
, то мы продолжаем делить отрезок до тех пор, пока длина отрезка не станет меньше 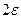 , тогда середина последнего отрезка дает значение корня с требуемой точностью.
, тогда середина последнего отрезка дает значение корня с требуемой точностью.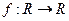 сжатие, то для него существует в R единственная неподвижная точка, к которой сходится итерационный процесс.
сжатие, то для него существует в R единственная неподвижная точка, к которой сходится итерационный процесс.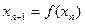 , где
, где 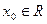 - произвольный.
- произвольный.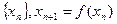 – фундаментальная
– фундаментальная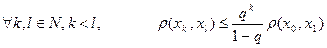 (*)
(*)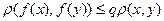 .
.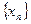 – сходится,
– сходится, 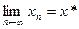 , причем
, причем 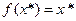 , т.е.
, т.е. 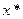 – неподвижная точка.
– неподвижная точка.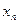 - последовательность приближения к решению уравнения
- последовательность приближения к решению уравнения 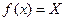
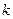 зафиксировать, а
зафиксировать, а 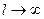 , то
, то – оценка погрешности, оценка скорости сходимости.
– оценка погрешности, оценка скорости сходимости.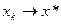 со скоростью геометрической прогрессии.
со скоростью геометрической прогрессии.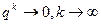 – линейная скорость сходимости.
– линейная скорость сходимости.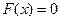 (2),
(2),  – вещественная функция.
– вещественная функция.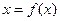 .
.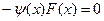 ,
, 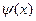 - знакопостоянная непрерывная функция.
- знакопостоянная непрерывная функция.