Метод секущих. Метод секущих имеет вид:Метод секущих имеет вид:
Скорость сходимости – сверхлинейная.
Метод секущих сходится быстрее метода хорд и метода простой итерации.
§15. Метод Гаусса решения систем уравнений. Для решения систем уравнений используют методы: точные и приближенные. К точным относятся: ü метод Гаусса; ü метод Крамера; ü метод оптимального исключения; ü метод квадратного корня. К приближенным методам решения систем уравнений относятся: ü метод простой итерации; ü метод Зейделя; ü метод Ньютона.
Метод Гаусса состоит в том, чтобы исходную систему вида Ах=b (1) с произвольной матрицей А свести к системе вида:
Процесс сведения системы (1) к системе (2) называется прямым ходом метода Гаусса. А нахождение неизвестных При вычислениях по методу Гаусса велика вероятность случайных ошибок. С целью избежать их вводится контрольный столбец:
Элементы контрольного столбца преобразовываются по тем же формулам, что и элементы матрицы А. Второй шаг контроля состоит в проверке равенства суммы элементов преобразованной строки и контрольного элемента. Эти величины должны совпадать с точностью до 1,2 единиц последнего разряда.
|
.
.
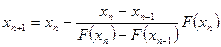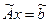(2), где 
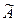- уже треугольная матрица.
- обратный ход метода Гаусса.
, где 
