Геометрический смысл метода Ньютона.
 Пусть требуется решить уравнение Пусть требуется решить уравнение 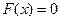 и единственный корень этого уравнения находится на и единственный корень этого уравнения находится на 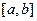 . .
В точке Если
Возьмем Если
И так далее. Отсюда метод Ньютона называют методом касательных.
§14. Метод хорд. Метод секущих. По прежнему решаем уравнение Т.е. на Уравнение (1) запишем в виде Тогда итерационный метод
Докажем, что метод хорд сходится. Для этого необходимо показать, что
Разложим
Рассмотрим при
Обозначим через
Т.е.
Следовательно, Получим оценку погрешности для метода хорд
Так как
Обозначим через Сходимость методы хорд – линейная. Достоинство метода хорд – легкость программирования на ЭВМ.
Общий вид упростится: ü При условии ü При условии
|


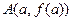 проведем касательную к графику функции
проведем касательную к графику функции 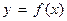 , уравнение касательной:
, уравнение касательной: 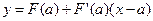 .
.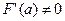 , то
, то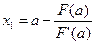 – первое приближение к
– первое приближение к 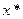 уравнения (1) по методу Ньютона.
уравнения (1) по методу Ньютона.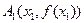 и проведем касательную в этой точке. Получим
и проведем касательную в этой точке. Получим 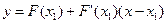 .
.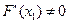 , то
, то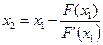 – второе приближение к
– второе приближение к 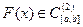 ,
, 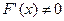 на
на 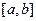 и
и 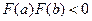 .
.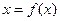 , где
, где 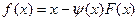 . Возьмем в качестве
. Возьмем в качестве 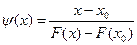 , где
, где 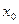 удовлетворяет условию
удовлетворяет условию 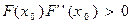 ,
, 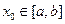 .
.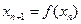 запишется следующим образом:
запишется следующим образом: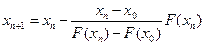 – метод хорд.
– метод хорд.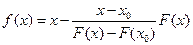 .
.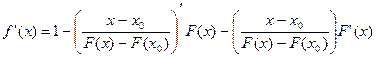
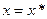
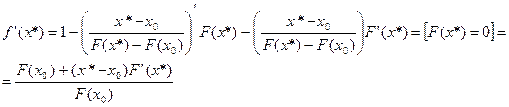
 в ряд Тейлора
в ряд Тейлора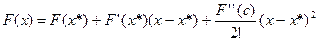 .
.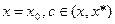 .
.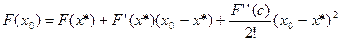
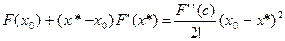
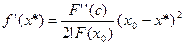 .
.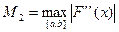
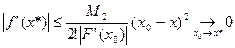
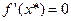 .
.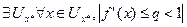 .
.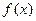 – сжатие и по принципу Банаха метод хорд сходится.
– сжатие и по принципу Банаха метод хорд сходится.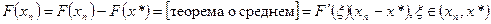
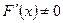 на
на 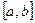 , то
, то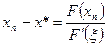 .
.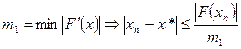 - оценка погрешности для метода хорд.
- оценка погрешности для метода хорд.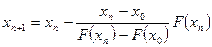 – общий вид метода хорд.
– общий вид метода хорд.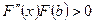 , то
, то 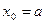 ,
, 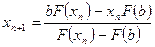 ;
;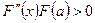 , то
, то 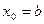 ,
, 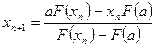 .
.


