Метод Ньютона. Решение уравнений с одной переменной.
Пусть требуется решить уравнение Из этих условий вытекает, что на Прежде, чем использовать итерации, необходимо (1) привести к виду
Функция В качестве Выберем начальное приближение
Метод, определенный (4), называется методом Ньютона. Докажем, что метод Ньютона сходится и получим его оценку погрешности.
Докажем, что (4) сходится. Для этого покажем, что отображение
При
По непрерывности функции Поэтому к отображению Если выбрать Заметим, что метод (4) будет сходиться, если начальное приближение
Докажем, что метод Ньютона сходится. Определим скорость сходимости метода Ньютона. Для этого
При
Выразим
Потребуем, чтобы начальное условие
Тогда из (6) получим
Метод Ньютона имеет квадратичную скорость сходимости. Это означает, что при переходе от одной итерации к другой количество верных знаков удваивается в последующем приближении. Достоинство: высокая скорость сходимости, легко программируется на ЭВМ. Недостатки: узкая область сходимости. Если будем решать операторное уравнение
|

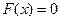 (1), где функция
(1), где функция  – дважды непрерывно-дифференцируема на
– дважды непрерывно-дифференцируема на 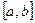 ;
;  на
на 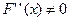 и
и 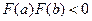 .
.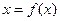 .
.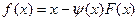 .
.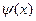 непрерывная в окрестности корня
непрерывная в окрестности корня 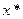 уравнения (1). Следовательно, уравнение (1) и уравнение
уравнения (1). Следовательно, уравнение (1) и уравнение  (2) будут иметь один и тот же корень
(2) будут иметь один и тот же корень 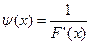 , тогда
, тогда  (3)
(3)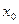 достаточно близкое к
достаточно близкое к 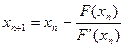 (4)
(4)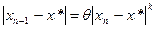 , где
, где 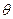 – символ Ландау:
– символ Ландау:
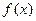 – сжатие, где
– сжатие, где 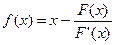 .
.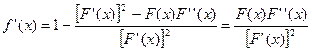 .
.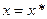 получим
получим .
.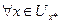 ,
, 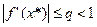 , а этом сжатие.
, а этом сжатие.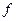 можно применить принцип сжатыхотображений.
можно применить принцип сжатыхотображений.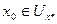 , то
, то 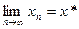 .
.
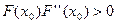 .
. разложим в ряд Тейлора в точке
разложим в ряд Тейлора в точке 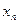 .
.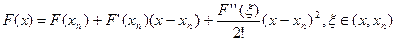 .
.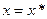 имеем
имеем 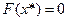 . Поэтому
. Поэтому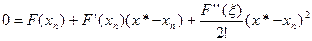
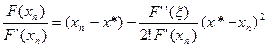 (5)
(5)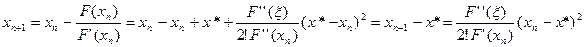 Обозначим через
Обозначим через 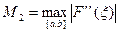 ,
, 
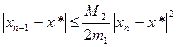 (6)
(6)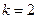 , скорость сходимости метода Ньютона квадратичная,
, скорость сходимости метода Ньютона квадратичная, 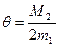 .
.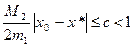 (7)
(7)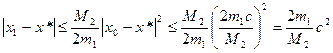

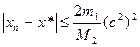 - оценка погрешности.
- оценка погрешности. .
.


