Решение уравнений с одним неизвестным. Дихотомия.
Пусть требуется решить уравнение Число Если функция Отделить корень уравнения значит найти такой интервал, внутри которого находится один и только один корень данного уравнения. Для отделения корней можно применить следующий признак: Если на отрезке Достаточным условием монотонности функции на отрезке является сохранение знака производной. Отделить корень можно и графически: нарисовать график и указать точки пересечения с осью Ох. Совершенный метод отделения корней – метод Штурма.
|
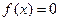(1), где 
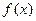– непрерывная функция.
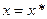называется корнем уравнения (1), если 
.
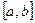и на концах отрезка принимает значения разных знаков, то на 
