Поэтому
1-я стадия работы: Постановка задачи. 2-я стадия работы: Математическое исследование. В зависимости от сложности модели применяют различные математические подходы, для наиболее грубых и наименее сложных моделей зачастую удается получить аналитическое решение (в виде формулы). Для наиболее точных и сложных моделей аналитическое решение удается получить крайне редко и тогда применяют численные методы решения, которые как правило требуют расчета на ЭВМ. 3-я стадия работы. Осмысление математического решения и его сопоставление с данными эксперимента. Если решение хорошо согласуется с данными эксперимента, то такую модель можно применять для расчета процессов данного типа (модель выбрана правильно), если же решение плохо согласуется с данными эксперимента, то такую модель необходимо пересмотреть и уточнить. Численные методы являются одним из мощных математических средств решения задач. Есть задачи, где без достаточно сложных численных методов не удалось бы получить ответа. В современной физике таких задач очень много, более того за короткое время нужно провести огромное количество вычислений, иначе нет смысла решать задачу (суточный прогноз погоды должен быть просчитан за несколько часов, а коррекция движения ракеты за несколько минут). Это немыслимо без мощных ЭВМ, выполняющих 1000000 операций в секунду. Современные численные методы и мощные ЭВМ позволили решать задачи, о которых полвека назад человек мог только мечтать. Численные методы делятся на точные и приближенные. Точные методы позволяют за конечное число арифметических действий получить решение задачи. При этом если исходные данные заданы точно и вычисления производились без округления, то получается точное решение задачи. К точным методам относятся: метод Гаусса и его модификации, метод Крамера, метод ортогонализации и т.д. Приближенные методы (итерационные) дают бесконечную последовательность приближений, предел которых, если он существует, является решением задачи. К итерационным методам относятся метод Ньютона и метод простых итераций, метод хорд и метод секущих для решений уравнений.
§9. Понятие корректно поставленной и некорректно поставленной задач. При приближенном решении математических или прикладных задач весьма существенным является вопрос о том, корректно ли решаемая задача. Большинство некорректных задач записывается в виде уравнения первого порядка, где по заданному необязательному оператору
Определение. Задача определения решения
Решение устойчиво, если бесконечно малым вариациям правой части соответствуют бесконечно малые вариации х.
Определение. Следуя Жаку Адамару задача отыскания 1. существует в Х; 2. единственно в Х; 3. устойчиво в Х. Если же хотя бы одно из условий 1-3 не выполняется, то задача некорректна.
§10. Вспомогательные сведения из функционального анализа. Определение. Множество Х произвольных элементов называется метрическим пространством, если 1. 2. 3.
1-3 – аксиомы метрики.
Говорят, что множество элементов
Последовательность точек Всякая сходящаяся последовательность является фундаментальной, обратное верно не всегда.
Определение. Метрическое пространство, в котором всякая фундаментальная последовательность сходится называется полным.
Пример. Зададим различными способами расстояния: 1. кубическая метрика, m-метрика
2. сферическая метрика,
3. октаэдрическая, s-метрика
Для всех выполняются аксиомы метрики и в каждой
Пусть X,Y – метрические пространства.
Если X=Y, то Если Определение. Говорят, что отображение
|

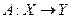 и по известной правой части
и по известной правой части 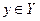 требуется найти
требуется найти 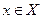 .
.
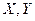 - метрические пространства, а в особо оговариваемых случаях – Банаховы или Гильбертовы.
- метрические пространства, а в особо оговариваемых случаях – Банаховы или Гильбертовы. при заданном
при заданном 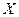 и
и 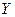 , если
, если 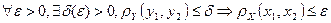

 (1)
(1)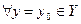 решение задачи:
решение задачи: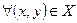 ставится в соответствие число
ставится в соответствие число  , удовлетворяющее следующим условиям:
, удовлетворяющее следующим условиям: ;
;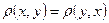 ;
;
 - метрическое пространство сходится к
- метрическое пространство сходится к 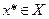 , если
, если 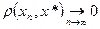
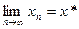 ,
, 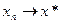 .
.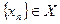 называется сходящейся в себе (фундаментальной), если
называется сходящейся в себе (фундаментальной), если 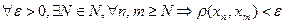 .
.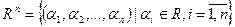 .
. ;
;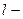 метрика
метрика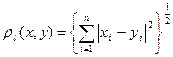 ;
; .
.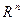 – полное метрическое пространство.
– полное метрическое пространство.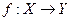 называется оператором, заданным в X со значением в Y.
называется оператором, заданным в X со значением в Y.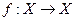 – оператор, отображающий Х в себя (преобразование).
– оператор, отображающий Х в себя (преобразование). , то
, то 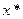 – неподвижная точка при отображении
– неподвижная точка при отображении 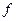 .
.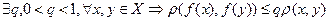 .
.


