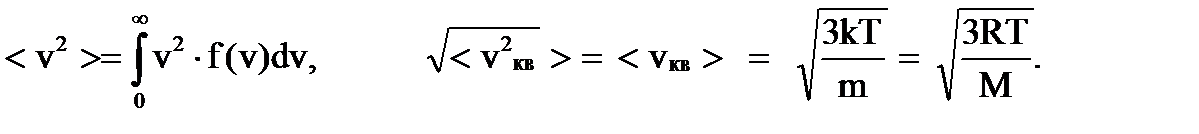По скоростям и энергиям теплового движения
Молекулы газа движутся хаотично. Величины и направления скоростей молекул изменяются в результате весьма частых (до 109 с-1) соударений с другими молекулами. Так как все направления движения равновероятны, то распределение молекул по направлениям будет равномерным, т.е. в каждом из выбранных направлений будет двигаться равное число молекул. Вместе с тем возможные численные значения скорости отнюдь неравновероятны, неодинаковы. Вследствие соударений с другими молекулами молекула может приобрести энергию существенно большую, чем ее средняя энергия < ε>. Однако, если одна молекула отберет энергию даже у всех остальных молекул, то и тогда ее энергия будет конечной, т.е. скорость молекулы газа вообще не может иметь значения выше некоторого значения vmax, а тем более v = ∞. Вероятности того, что скорости слишком большие и слишком малые по сравнению со средней, практически невелики и значения скоростей группируются около некоторого наиболее вероятного значения. Воспользуемся способом моментальной “фотографии“. Возьмем горизонтальную ось скоростей. Крестиками на оси скоростей отметим значения скоростей молекул, зафиксированные в какой-то момент времени. Качественная картина распределения молекул вдоль оси скоростей будет такой, как на рис.52. Плотность точек ρ (как она обозначена формулой 9.1) вдоль оси будет неравномерной и, очевидно, будет зависеть от величины скорости v, так как зависит от выбора места интервала скоростей Δv
где Δv - интервал скоростей от v до (v + Δv); ΔNv - число молекул, обладающих скоростями в интервале значений от v до (v + Δv). Если взять несколько порций газа при одинаковых давлении P и температуре Т в идентичных условиях, то плотность точек на оси v будет пропорциональна числу молекул N в каждой порции газа, а одинаковым для всех порций газа будет отношение
Функция f(v) называется функцией распределения молекул по скоростям. Величина Сумма этой величины по всему диапазону скоростей от 0 до ∞ будет равна 1:
Вид функции распределения молекул по скоростям получен Максвеллом и она носит его имя
где m - масса молекулы, k - постоянная Больцмана, T -температура, А - множитель, который не зависит от скорости. Величины
Коэффициент А находят из условия нормировки.
Этот интеграл будет равен 1, когда коэффициент А будет равен
и тогда окончательный вид функции распределения будет
График функции дан на рис. 53. Эта функция зависит от рода газа (m) и параметра состояния (Т). Давление и объем на функцию распределения f (v) не влияют. Скорость, отвечающая максимуму распределения, называется вероятной vвер и является наиболее вероятной. Выражение для vвер можно получить продифференцировав
При v=0 и v=∞ функция имеет минимумы, а из условия
отвечающее условию максимума функции при v=vвер.
С ростом температуры максимум распределения смещается в сторону больших скоростей (рис. 54).
Зная распределение молекул по скоростям, можно найти среднее значение скорости <vар> (среднее арифметическое), а также среднее значение квадрата скорости <v2кв>.
Оценка средней скорости молекул кислорода (М=32 кг/кмоль) при нормальных условиях даст величину порядка 500м/с, а для водорода порядка 2 км/с. Относительные количества молекул ΔN/N для различных интервалов скоростей приведены в таблице
Как видно из таблицы, более чем у 70% всех молекул скорость отличается от наиболее вероятной не больше, чем на 50%. Скоростью, более чем в
|
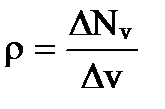, (9.1)
дает вероятность того, что скорость молекулы будет иметь значение в пределах данного интервала скоростей Δv.
Поскольку скорость молекулы обязательно имеет какую - то величину (от 0 до ∞), вероятность этого есть вероятность достоверного события, которая, следовательно, равна 1, т.е.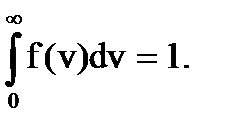
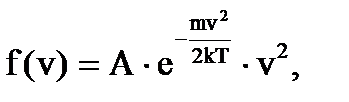
стоящие в показателе степени, характеризуют среднее значение энергии молекулы. Экспонента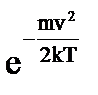 
убывает быстрее, чем возрастает v2, поэтому функция f (v) (рис. 53), достигнув максимума, будет ассимптотически стремиться к нулю.
,
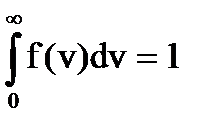и приравняв эту производную нулю.
.
.
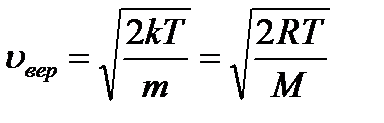