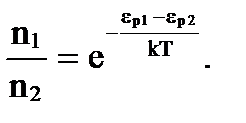Распределение Больцмана
Атмосферное давление на высоте h обусловлено весом вышележащих слоев газа. Пусть Р давление газа на высоте h. Тогда давление на высоте h+dh будет P+dP, а разность давлений dP будет равна весу газа mg в объеме V с площадью основания S = 1 м2 и высотой dh (V=Sdh), отнесенному к S. Выразим плотность газа ρ через давление P из уравнения Менделеева-Клапейрона
Тогда
Проинтегрируем отдельно левую и правую части уравнения. Считая температуру постоянной T=const, получим
где С – постоянная интегрирования. Выражение для давления будет
Это уравнение носит название барометрической формулы и показывает зависимость давления газа от высоты. Видно, что чем тяжелее молекулы и чем ниже температура, тем быстрее уменьшается давление с увеличением высоты. Заменим в формуле давление, выразив его через концентрацию молекул из уравнений P = nkT, P0 = n0kT и
где n0 - концентрация молекул на высоте h=0; n - концентрация молекул на высоте h≠0. Данная формула описывает изменение концентрации молекул от высоты h в потенциальном поле земного тяготения и от температуры Т. Можно отметить две тенденции, определяющих распределение молекул по высоте: 1. Притяжение молекул к Земле (mg) стремится расположить их на поверхности Земли. 2. Тепловое движение (kT) стремится разбросать молекулы равномерно по всем высотам от 0 до В результате этих конкурирующих процессов распределение молекул газа по высоте имеет промежуточный вид. Потенциальная энергия молекулы e=mgh. Следовательно, полученная формула представляет собой распределение молекул по значениям потенциальной энергии
Это формула распределения Больцмана. Здесь n0 концентрация молекул в том месте, где eР = 0, n –концентрация молекул в той точке пространства, где молекула обладает потенциальной энергией ep~0. Молекулы стремятся расположиться с наибольшей плотностью там, где у них минимальная потенциальная энергия
Закон Максвелла дает распределение молекул по значениям кинетической энергии, а закон Больцмана - по значениям потенциальной энергии. Больцман доказал, что формула распределения справедлива не только в случае потенциального поля земного тяготения, но и в любом потенциальном поле сил для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения. Глава 7. Основы термодинамики
|




 ,
,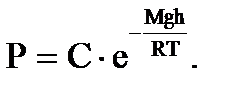 Постоянную интегрирования определяют из граничного условия. Если h = 0, то С = Р0 и тогда
Постоянную интегрирования определяют из граничного условия. Если h = 0, то С = Р0 и тогда

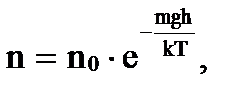
 .
.