Основное уравнение молекулярно-кинетической теории газов
В молекулярно-кинетической теории используют идеализированную модель идеального газа. Газ называется идеальным, если при рассмотрении его свойств соблюдаются следующие условия: 1. Столкновения молекул такого газа между собой и со стенками сосуда происходят как соударения упругих шаров; 2. Размеры молекул и их собственный суммарный объем пренебрежимо малы по сравнению с размерами и объемом сосуда; 3. Между молекулами не проявляются силы взаимного притяжения. Эти условия выполняются для всех газов при не слишком высоких давлениях и не слишком низких температурах, поэтому при условиях, близких к нормальным, газ можно считать идеальным. Рассмотрим процесс взаимодействия движущихся молекул со стенками сосуда, в котором находится идеальный одноатомный газ. Возьмем сосуд в форме куба с ребром l. В сосуде находится однородный газ. Так как движение носит хаотический характер, то ни одно направление движения не имеет преимущества перед другими. Поэтому можно считать, что в каждом из 3-х направлений движется 1/3 общего числа n молекул, содержащихся в сосуде, [(1/3) ∙ n]. Пусть масса отдельной молекулы m, а скорость v направлена по нормали к грани куба. При упругом ударе молекулы о стенку изменится направление скорости на противоположное и молекула будет двигаться к противоположной грани куба. Изменение импульса молекулы Δp при столкновении со стенкой сосуда равно Δp = mv – (-mv) = 2mv, что будет соответствовать импульсу силы f, с которой отдельная молекула воздействовала на стенку, а стенка на молекулу f Δt=2mv. Пройдя путь, равный l и отразившись от противоположной грани, молекула через время Δt=2 l /v вновь столкнется с рассматриваемой гранью куба. Таким образом, средняя сила, с которой отдельная молекула воздействует на грань сосуда, будет
Так как газ в сосуде однородный, то m1 = m2 = m3 =…= m, т.е. массы молекул равны. Но молекулы имеют разные скорости v1, v2, v3, …, vn и между двумя противоположными гранями движется 1/3 всех n молекул, находящихся в сосуде. Значит, суммарная сила ударов 1/3 всех n молекул об одну грань куба будет:
Перепишем это выражение, домножив числитель и знаменатель на число молекул n и, сделав некоторые преобразования, получим
Величину
где
Кинетическая энергия и скорость поступательного движения молекулы. Давление. Уравнение (8.1) можно представить в виде
Величина
Пусть в объеме V находится 1 моль газа. 1 моль газа содержит число молекул, равное числу Авагадро NA=6 1023 моль-1. Тогда концентрация молекул n0 =NA/V и уравнение (8.2) принимает вид
Уравнение Менделеева-Клапейрона для 1 моля газа имеет вид PV = RT, откуда
Отсюда выражение для средней кинетической энергии молекулы ε будет где
В соответствии с этим, нуль абсолютной температуры приобретает следующий смысл: - при абсолютном нуле отсутствует поступательное движение молекул (хотя остаются другие виды движения, например, внутриатомные), т.к. при Т=0 энергия молекулы ε=0, а следовательно, и ее скорость v=0. Сама абсолютная температура является мерой движения молекул. Найдем выражение для среднеквадратичной скорости молекулы. Приравняем энергию молекулы, выраженную через температуру и скорость.
Учитывая что
Для воздуха при комнатной температуре <vкв> Давление газа прямопропорционально концентрации молекул n0 и его абсолютной температуре Т. Это уравнение можно получить непосредственно из уравнения состояния газа – уравнения Менделеева-Клапейрона. Выразим из этого уравнения давление
Домножим числитель и знаменатель на число Авагадро NA, и учитывая,что m/M, умноженное на NA есть число молекул n в объеме V, а
|




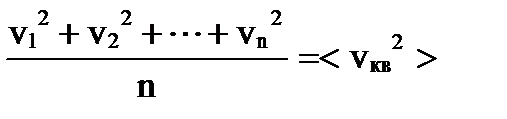 называют среднеквадратичной скоростью молекул. Тогда
называют среднеквадратичной скоростью молекул. Тогда  . Разделив обе части на S= l 2 площадь грани куба, получим в левой части давление P, а в правой выражение для него
. Разделив обе части на S= l 2 площадь грани куба, получим в левой части давление P, а в правой выражение для него (8.1)
(8.1)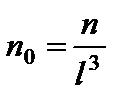 - концентрация молекул- содержание (количество) молекул в единице объема. Выражение (8.1) представляет собой основное уравнение молекулярно-кинетической теории газов. Это уравнение связывает макроскопическую величину P с числом молекул в единице объема, массой молекулы и ее среднеквадратичной скоростью движения.
- концентрация молекул- содержание (количество) молекул в единице объема. Выражение (8.1) представляет собой основное уравнение молекулярно-кинетической теории газов. Это уравнение связывает макроскопическую величину P с числом молекул в единице объема, массой молекулы и ее среднеквадратичной скоростью движения. .
. представляет собой среднюю кинетическую энергию поступательного движения отдельной молекулы. Тогда давление P можно записать в виде:
представляет собой среднюю кинетическую энергию поступательного движения отдельной молекулы. Тогда давление P можно записать в виде: . (8.2)
. (8.2) .
. .
.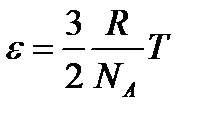 ,
, - есть отношение двух постоянных величин и представляет собой постоянную величину, называемую постоянной Больцмана
- есть отношение двух постоянных величин и представляет собой постоянную величину, называемую постоянной Больцмана  С учетом этого средняя кинетическая энергия поступательного движения отдельной молекулы связана с температурой Т соотношением
С учетом этого средняя кинетическая энергия поступательного движения отдельной молекулы связана с температурой Т соотношением .
. Отсюда <vкв>=
Отсюда <vкв>= 


 500м/с. Следовательно, если известна температура газа и его молярная масса (т.е. вид газа), то можно найти среднеквадратичную скорость его молекул. Объединяя формулы
500м/с. Следовательно, если известна температура газа и его молярная масса (т.е. вид газа), то можно найти среднеквадратичную скорость его молекул. Объединяя формулы  и
и  , получим выражение для давления
, получим выражение для давления 
 .
. -постоянная Больцмана, получим
-постоянная Больцмана, получим



