Вычисление портфельного риска

Убедившись, что диверсификация снижает риск, целесообразно сделать следующий шаг - научиться рассчитывать доходность и риск портфеля.

Допустим, что мы сформировали портфель из акций двух компаний, первой и второй, соответственно, в пропорции 60 и 40%. Ожидается, что годовая доходность акции первой компании будет равна 15%, акции второй - 21%. Как уже отмечалось, ожидаемая доходность портфеля равна средневзвешенной доходности представленных в нем акций

.

Расчет стандартного отклонения портфеля значительно более сложен. В теории вероятности доказывается, что дисперсия суммы случайных величин рассчитывается по следующей формуле

.

Здесь: γ_i и γ_j - доли случайных величин i и j в общей сумме;

σ_i и σ_j - среднеквадратические отклонения этих величин;

ρ_i,j - коэффициент корреляции этих величин[32].

Не вдаваясь в область теории вероятности и математической статистики, проиллюстрируем алгоритм расчета дисперсии пакета акций на конкретном примере, представив его в виде удобной таблицы.

Таблица 7.4.

Алгоритм расчета стандартного отклонения пакета из акций двух предприятий

	Акция 1	Акция 2
Акция 1
Акция 2

В таблице использованы следующие обозначения:

γ_i - доля акции i-ой компании в пакете;

σ_i - среднеквадратичное отклонение доходности акции i-ой компании;

ρ_i,j - коэффициент корреляции доходностей акций i -ой и j -ой компаний.

Дисперсия портфеля равна сумме всех четырех клеток таблицы:

.

Приведенное соотношение показывает, что стандартное отклонение доходности пакета зависит от величины стандартных отклонений доходности отдельных акций и их корреляции. Если изменения доходностей акций соответствуют друг другу, то есть при росте одной акции растет и вторая, то коэффициент корреляции положителен. Если доходности изменяются в противоположных направлениях, то коэффициент корреляции отрицательный. Если изменения доходностей никак не связаны, то корреляция равна нулю. Соответственно равен нулю и коэффициент корреляции. Следует заметить, что доходности большинства акций имеют тенденции к согласованному изменению, поэтому теоретическая возможность нулевой дисперсии, а стало быть, и нулевого риска пакета, практически нереализуема. Однако их коэффициенты корреляции практически всегда меньше единицы,[33] что и обеспечивает снижение риска пакета.

Воспользуемся приведенным алгоритмом и рассчитаем стандартное отклонение доходности рассмотренного ранее пакета из двух акций. Напомним, что пакет на 60% состоит из акций первого вида и на 40% - из акций второго вида. Пусть стандартные отклонения доходностей этих акций равны 28 и 42%, соответственно, а коэффициент корреляции между ними равен 0,6.

Таблица 7.5.

Расчет стандартного отклонения пакета из акций двух предприятий

	Акция 1	Акция 2
Акция 1	0,360*0,078 = 0,028	0,6*0,4*0,6*0,28*0,42 = 0,017
Акция 2	0,017	0,160*0,176 = 0,028

В соответствии с табличными данными, среднеквадратическое отклонение доходности пакета акции будет равно 30%. Таким образом, в результате диверсификации мы получим пакет с достаточно высокой ожидаемой доходностью 17,4%, при риске практически равном риску низкодоходных акций первой компании. Необходимые для такой оценки статистические характеристики доходностей отдельных акций могут быть получены с помощью ретроспективного анализа.

Алгоритм вычисления дисперсии пакета из N акций соответствует построению матрицы NxN, где по диагонали будут находиться взвешенные по квадрату доли в пакете дисперсии акций от 1 до N, а в остальных клетках произведения долей, коэффициентов корреляции и среднеквадратических отклонений пакетов с номерами соответствующими рассматриваемой строке и столбцу матрицы. В соответствии с приведенным алгоритмом, дисперсия пакета из N акций определяется по соотношению

.

Рассмотрим портфель с равными долями из N акций. Дисперсия такого пакета будет равна

.

Обозначив σ² = D (дисперсия), а ρ_i,jσ_i,jσ_i,j = COV_i,j (ковариация), запишем

.

Из рассмотренного примера хорошо видно, что при возрастании N дисперсия портфеля стремится к среднему значению ковариации, и если бы было возможно формирование пакета с нулевой ковариацией, то можно было бы получить нулевой риск ожидаемой доходности. Но, к сожалению, это невозможно, и не только потому, что реальные характеристики доходности могут не соответствовать прогнозируемым. Сама суть рыночной экономики такова, что большинство акций корпораций имеют положительную ковариацию, которая ограничивает эффект диверсификации.

Проведенный анализ раскрывает смысл индивидуальной и рыночной составляющих риска пакета акций (см. рис. 7.4).
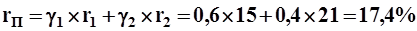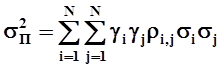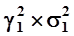
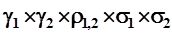
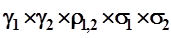
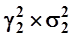
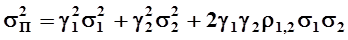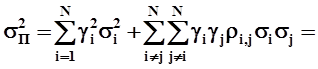
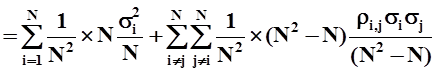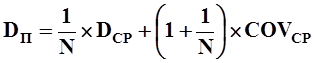