Частные случаи динамической теоремы Кориолиса.
Инерциальная система координат
2.1. Подвижные оси перемещаются поступательно, равномерно и прямолинейно
т.е. закон относительного движения имеет такой же вид, как и в неподвижной системе координат. Система координат, которая движется относительно «неподвижной» поступательно, равномерно и прямолинейно, называется инерциальной. В инерциальной системе координат материальная точка может получить ускорение только вследствие реального воздействия на точку других точек (тел). С другой стороны, инерциальную систему координат можно определить как такую подвижную систему, по отношению к которой динамические дифференциальные уравнения движения имеют тот же вид, что и в неподвижной системе координат, т.е. без учета переносной силы и кориолисовой силы инерции. В этом состоит принцип относительности классической механики Галилея-Ньютона.
2.2. Точка по отношению к подвижным осям движется равномерно и прямолинейно. Это значит
2.3. Точка по отношению к подвижным осям находится в покое (относительное равновесие). В этом случае
Уравнение относительного равновесия составляются так же, как уравнения равновесия в неподвижных осях, если при этом к действующим на точку силам взаимодействия с другими телами добавить переносную силу инерции. Замечание. Отметим различие понятия об условиях равновесия точки в инерциальной и неинерциальной системах отсчета. В инерциальной условие равновесия означает, что точка находится в состоянии покоя или равномерного прямолинейного движения. Состояние покоя точки и равномерного прямолинейного движения описываются равными уравнениями (8) и (7).
|

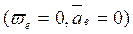 . В этом случае
. В этом случае 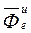 = 0,
= 0, 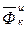 = 0.
= 0.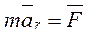 , (6)
, (6)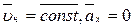 . Уравнение равномерного прямолинейного движения относительного движения точки примет вид
. Уравнение равномерного прямолинейного движения относительного движения точки примет вид (7)
(7) ,
, 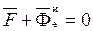 (8)
(8)


