Уклонение линии отвеса от направления радиуса Земли
Пусть материальная точка М массы m подвешена на нити вблизи Земной поверхности и находится в относительном покое под действием трех сил: гравитационной силы притяжения к Земле
Откуда Силу, равную по модулю и направленную противоположно натяжению нити
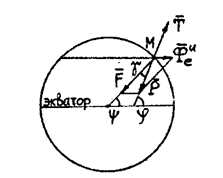
Рис. 2
Наблюдаемый на поверхности Земли вес материальной точки есть равнодействующая силы притяжения материальной точки к Земле и переносной силы инерции этой точки. Линия действия силы Угол Спроектируем уравнение (9) на направление нити и перпендикуляр к этому направлению
Пренебрегая малой величиной
Или Из второго уравнения системы (10) находим Из приведенных вычислений следует: 1. Ускорение силы тяжести на поверхности Земли g меньше гравитационного ускорения 2. Направление истинной вертикали совпадает с радиусом Земли лишь на полюсе и на экваторе 3. Введением в уравнения равновесия силы тяжести 4. Переносной силой инерции, вызванной вращением Земли, объясняется так же и сжатие Земли. Земля имеет форму геоида, т.е. тела, нормаль к поверхности которого совпадает в каждой точке с линией отвеса.
|

 , натяжения нити
, натяжения нити 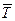 , и силы инерции переносного движения
, и силы инерции переносного движения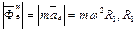 - расстояние точки М от земной оси (рис.2). Как известно, сила притяжения к Земле пропорциональна квадрату расстояния между ними (
- расстояние точки М от земной оси (рис.2). Как известно, сила притяжения к Земле пропорциональна квадрату расстояния между ними (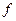 - гравитационная постоянная,
- гравитационная постоянная,  - масса Земли, R – радиус Земли).
- масса Земли, R – радиус Земли).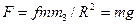 . Учитывая, что
. Учитывая, что 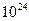 кг,
кг, 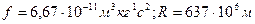 , для гравитационного ускорения получим
, для гравитационного ускорения получим 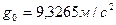 . Уравнение относительного равновесия токи записывается в виде:
. Уравнение относительного равновесия токи записывается в виде: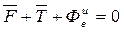 . (9)
. (9)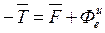 .
.
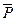 называется вертикалью в данном месте земной поверхности, а плоскость, перпендикулярная к вертикали, называется горизонтальной плоскостью.
называется вертикалью в данном месте земной поверхности, а плоскость, перпендикулярная к вертикали, называется горизонтальной плоскостью.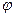 , составленный вертикалью с плоскостью экватора, называется географической широтой в данном пункте земной поверхности. Из рис. 2 видно, что вертикаль отклоняется от радиуса Земли на угол γ.
, составленный вертикалью с плоскостью экватора, называется географической широтой в данном пункте земной поверхности. Из рис. 2 видно, что вертикаль отклоняется от радиуса Земли на угол γ. (10)
(10)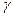 по сравнению с углом
по сравнению с углом 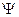 , получим
, получим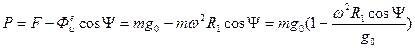
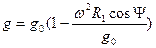

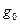 и зависит от положения точки на земной поверхности.
и зависит от положения точки на земной поверхности.


