Отклонение падающих тел к востоку от вертикали
Пусть точка М массы m падает без начальной скорости на Землю с высоты Н. Сопротивлением воздуха будем пренебрегать, а величину Н считаем малой по сравнению с радиусом Земли и поэтому не учитываем зависимость силы веса от расстояния. Возьмем систему координат, жестко связанную с Землей. Начало координат «О» совместим с точкой поверхности Земли, лежащей на одной вертикали с начальным положением Для составления уравнения относительного движения к силе
Учитывая, что
Рис. 6
Начальные условия при Так как сила Кориолиса очень мала по сравнению с силой тяжести, то в первом приближении можно считать вектор скорости направленным по вертикали, т.е. вдоль линии Тогда
Используя начальные условия (16), решение системы дифференциальных уравнений (17) представим в виде
Найдем максимальное отклонение точки к востоку. При z=0 находим
Подставляя
Неоднократно проводившиеся опыты подтверждают наличие восточного отклонения, близкого к теоретическому значению.
|

 падающего тела. Ось Z направим по истинной вертикали вверх, проведя ее через положение, занимаемое точкой в начальный момент времени. Ось X проведем по касательной к меридиану с севера на юг, ось У – по касательной к параллели с запада на восток (рис. 6). Полученную систему координат с достаточной степенью можно считать прямоугольной.
падающего тела. Ось Z направим по истинной вертикали вверх, проведя ее через положение, занимаемое точкой в начальный момент времени. Ось X проведем по касательной к меридиану с севера на юг, ось У – по касательной к параллели с запада на восток (рис. 6). Полученную систему координат с достаточной степенью можно считать прямоугольной. (притяжение Земли), нужно добавить силу инерции переносную
(притяжение Земли), нужно добавить силу инерции переносную  и силу инерции Кориолиса
и силу инерции Кориолиса 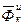 , причем
, причем
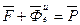 , уравнение относительного движения запишем в виде
, уравнение относительного движения запишем в виде  или проекциях на оси х, у, z.
или проекциях на оси х, у, z.
 (15)
(15)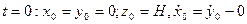 (16)
(16)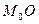 .
. и уравнения (15) примут вид
и уравнения (15) примут вид . (17)
. (17)
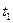 - время, за которое тело упадет на землю:
- время, за которое тело упадет на землю: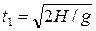 .
.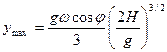 .
. Пусть
Пусть  тогда
тогда  = 12,55 мм.
= 12,55 мм.


