I. Динамические дифференциальные уравнения относительного движения материальной точки
Динамика относительного движения точки Методические указания для иностранных студентов
Ростов-на-Дону
УДК 531.01
Динамика относительного движения точки: Методические указания для иностранных студентов. – Ростов н/Д: Ростовский государственный строительный университет, 2007. – 19 с.
Предназначены для иностранных студентов, испытывающих трудности при записи лекций по теоретической механике. Даны основные определения, формулировки теорем. Рассмотрены типовые задачи. УДК 531.01
Составитель: канд. физ.-мат. наук М.Ю. Ремизов Рецензент: канд.физ.-мат. наук Е.Б. Русакова
Редактор Т.М. Климчук Темплан 2007 г., поз. 157 Подписано в печать 08.06.07. Формат 60х84/16. Ризограф. Бумага писчая. Уч.- изд. л. 1,0. Тираж 50 экз. Заказ 309. Редакционно-издательский центр Ростовского государственного строительного университета 344022, Ростов н/Д, ул. Социалистическая, 162
© Ростовский государственный строительный университет, 2007 I. Динамические дифференциальные уравнения относительного движения материальной точки Известно, что силы, действующие на точку и являющиеся результатом взаимодействия ее с другими телами, не зависят от выбора системы координат и определяются соответствующими физическими законами взаимодействия. Например, сила тяготения зависит от масс взаимодействующих тел и расстояния между ними; сила упругости – от величины деформации пружины; сила сопротивления среды – от скорости тела относительно среды. Массы тел, расстояния между точками, деформации пружины в классической механике во всех системах координат – одни и те же величины. Ускорение точки зависит, как известно из кинематики, от выбора системы координат. Следовательно, закон, связывающий ускорение материальной точки и действующие на нее силы, не инвариантен относительно выбора системы отчета. Обозначим равнодействующую всех непосредственно приложенных к рассматриваемой материальной точке сил вектором
В качестве «неподвижной» может быть взята система координат, начало которой находится в центре инерции Солнечной системы, а оси направлены к трем неподвижным звездам. В инженерной практике часто встречаются задачи, когда требуется изучить движение материальной точки (тела) по отношению к подвижному пространству. Например, движение подвижных частей приборов, установленных на движущихся объектах, расчет траекторий космических летательных аппаратов по отношению к подвижным системам координат, связанным с планетами, и др. Постановка задачи. Зная действующие на точку силы и движение подвижной системы координат, найти закон относительного движения точки. Пусть
Y X Рис. 1
Напомним, что движение точки М относительно подвижной системы координат называется относительным; движение точки М вследствие движения подвижного пространства называется переносным; движение точки М относительно неподвижной системы координат называется абсолютным. Из кинематики известно, что самое общее движение свободного твердого тела (мы его связываем с подвижной системой координат) можно представить состоящим из поступательного движения вместе с какой-либо тела (А) и вращательного движения вокруг этой точки. Абсолютное ускорение т. М находится по формуле
Здесь Подставляя (2) в (1), после простых преобразований получим
Введем обозначения:
Величины
Уравнение (5) выражает основной закон динамики для относительного движения (динамическая теорема Кориолиса). В подвижной системе отсчета основной закон динамики не выполняется; но если к действующим на точку силам взаимодействия с другими материальными точками присоединить переносную и кориолисову силы инерции Важно понимать, что в неподвижной системе отсчета материальная точка может иметь ускорение только вследствие одной причины – действия на нее сил, т.е. взаимодействия с другими материальными телами. В подвижной системе отсчета причин две: действие сил (динамическая причина) и движение самой системы отсчета (кинематическая причина). Действительно пусть
т.е. точка будет иметь ускорение по отношению к подвижной системе только за счет движения последней, а не в результате действия каких-то сил. Таким образом, невыполнение в подвижной с.к. основного закона динамики связано с тем, что по отношению к этой системе точка получает ускорение не только в результате действия силы, но и вследствие движения самой системы отсчета.
|

 . Эти силы создают абсолютное ускорение
. Эти силы создают абсолютное ускорение 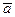 точки в «неподвижной» системе координат. Уравнение движения точки
точки в «неподвижной» системе координат. Уравнение движения точки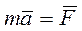 (1)
(1) - условно неподвижная система координат (с.к.), x,y,z - подвижная с.к. (рис. 1). M
- условно неподвижная система координат (с.к.), x,y,z - подвижная с.к. (рис. 1). M 


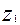

 Z
Z A
A 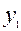
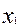

 O
O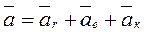 , (2)
, (2)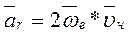 где
где 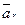 ,
, 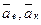 - соответственно относительное, переносное и кориолисово ускорения, причем относительное ускорение находится по формулам кинематики точки, переносное – как ускорение точки свободного твердого тела, ускорение Кориолиса – по формуле
- соответственно относительное, переносное и кориолисово ускорения, причем относительное ускорение находится по формулам кинематики точки, переносное – как ускорение точки свободного твердого тела, ускорение Кориолиса – по формуле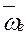 - угловая скорость переносного движения,
- угловая скорость переносного движения, 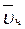 - относительная скорость точки.
- относительная скорость точки.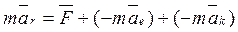 . (3)
. (3)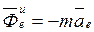 ,
, 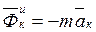 . (4)
. (4)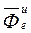 ,
, 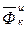 по размерности являются силами. Назовем их соответственно переносной и кориолисовой (поворотной) силами. Тогда предыдущее уравнение примет вид
по размерности являются силами. Назовем их соответственно переносной и кориолисовой (поворотной) силами. Тогда предыдущее уравнение примет вид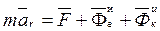 . (5)
. (5) (на точку силы не действуют или они уравновешены), тогда
(на точку силы не действуют или они уравновешены), тогда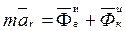 ,
,


