Точка массы m движется без трения по меридиану вращающейся Земли, принимаемой за шар (рис. 5а). Пусть 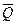 - сила, приложенная к рассматриваемой точке в направлении касательной к меридиану,
- сила, приложенная к рассматриваемой точке в направлении касательной к меридиану, 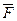 - сила тяготения точки к Земле,
- сила тяготения точки к Земле, 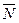 - реакция идеальной связи. Она расположена в плоскости, нормальной к меридиану, и ее можно разложить на две составляющие: вертикальную
- реакция идеальной связи. Она расположена в плоскости, нормальной к меридиану, и ее можно разложить на две составляющие: вертикальную  и горизонтальную
и горизонтальную 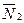 . Вертикальная составляющая при
. Вертикальная составляющая при 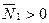 направлена по продолжению радиуса Земли вверх, а горизонтальная, если
направлена по продолжению радиуса Земли вверх, а горизонтальная, если 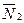 >0 - к западу по касательной к параллели того места, где в данное мгновение находится материальная точка.
>0 - к западу по касательной к параллели того места, где в данное мгновение находится материальная точка.
Обозначим угол между исходящим из центра Земли радиусом-вектором местоположения точки и плоскостью экватора через 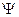 - геоцентрическая широта места. Отличие геоцентрической широты от географической (угол между той же плоскостью и истинной вертикалью места) – шесть дуговых минут на широте Парижа; R – радиус Земли;
- геоцентрическая широта места. Отличие геоцентрической широты от географической (угол между той же плоскостью и истинной вертикалью места) – шесть дуговых минут на широте Парижа; R – радиус Земли; 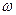 -угловая скорость Земли. За относительное движение примем перемещение точки по отношению к Земле, или, что то же, по отношению к географической сетке меридианов и параллелей, вращающейся вместе с Землей. Относительная скорость направлена по касательной к меридиану (рис. 5). Ее величина
-угловая скорость Земли. За относительное движение примем перемещение точки по отношению к Земле, или, что то же, по отношению к географической сетке меридианов и параллелей, вращающейся вместе с Землей. Относительная скорость направлена по касательной к меридиану (рис. 5). Ее величина 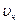 определяется формулой
определяется формулой
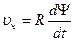 .
.
Переносная скорость точки равна скорости ее местоположения на вращающейся Земле и направлена по касательной к параллели места
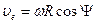 .
.
Относительное ускорение точки 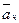 состоит из двух составляющих: тангенциальной
состоит из двух составляющих: тангенциальной 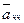 и нормальной
и нормальной 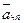 , соответственно направленных по касательной к меридиану и к центру Земли
, соответственно направленных по касательной к меридиану и к центру Земли
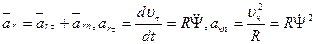 .
.
Бинормаль траектории точки в ее относительном движении совпадает с касательной к параллели места. За положительное направление примем бинормали на запад. Составляющая  . Переносное ускорение
. Переносное ускорение 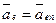 направлено к центру параллели (перпендикулярно оси Земли).
направлено к центру параллели (перпендикулярно оси Земли).
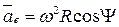
б I – параллель, II – меридиан
а
Рис. 5
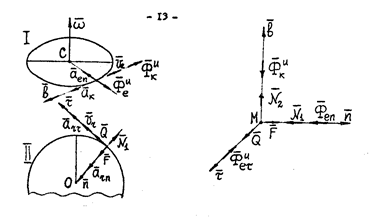
Проекции сил, действующих на точку М, на естественные оси
Переносная сила инерции направлена по продолжению радиуса параллели противоположно вектору 
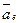 :
:
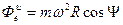 .
.
Проекции силы инерции переносного движения на касательную, нормаль и бинормаль к траектории относительного движения находятся по формулам
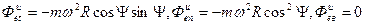 .
.
Кориолисово ускорение определяется формулой
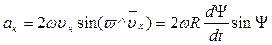 .
.
Оно направлено по касательной к параллели места и при этом так, чтобы, глядя с конца этого вектора на его начало, видеть кратчайший поворот от вектора 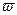 к вектору
к вектору 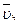 происходящим против хода часовой стрелки (Нетрудно проверить, что к тому же приводит правило Жуковского). Пусть
происходящим против хода часовой стрелки (Нетрудно проверить, что к тому же приводит правило Жуковского). Пусть  , тогда точка движется к северу, и ее кориолисово ускорение направленно на запад. Кориолисова сила инерции направлена на восток
, тогда точка движется к северу, и ее кориолисово ускорение направленно на запад. Кориолисова сила инерции направлена на восток
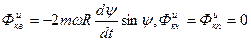 .
.
Уравнения относительного движения точки в векторной форме
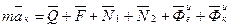 .
.
Проектируя это векторное уравнение на оси естественного трехгранника (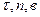 ), получим
), получим
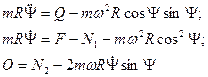 (11)
(11)
Первое из полученных уравнений не содержит реакции идеальной связи. Интегрируя это дифференциальное уравнение при заданных значениях переменной 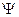 и
и 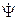 в начальный момент времени, можно найти широту
в начальный момент времени, можно найти широту 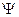 как функцию времени t. После этого второе и третье уравнения позволяют найти величины N
как функцию времени t. После этого второе и третье уравнения позволяют найти величины N 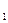 и N
и N  :
:
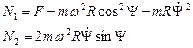
N  и N
и N  - реальные силы. Они приложены к движущейся материальной точке и представляют собой воздействие на точку со стороны связи (такой силой являются, например, давление проволоки, изогнутой по меридиану, на нанизанную бусинку, движущуюся при отсутствии атмосферы и трения скольжения).
- реальные силы. Они приложены к движущейся материальной точке и представляют собой воздействие на точку со стороны связи (такой силой являются, например, давление проволоки, изогнутой по меридиану, на нанизанную бусинку, движущуюся при отсутствии атмосферы и трения скольжения).
В свою очередь материальная точка на основании III закона Ньютона производит давление на связь с той же, но противоположно направленной силой. Если точка в северном полушарии движется к северу (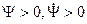 ), то
), то 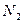 > 0. Это означает, что она направлена на запад, или, что то же, влево, если смотреть по направлению движения точки относительно земли. Соответственно материальная точка производит давление на связь вправо по отношению к направлению своей относительной скорости. Такое же положение сохраняется и при движении к югу. Можно показать (проделайте это!), что при движении точки по земной сфере по заданной криволинейной связи в северном полушарии материальная точка производит давление на связь вправо по направлению относительной скорости. Как известно, именно это обстоятельство лежит в основе объяснения подмыва реками своих правых берегов, образования циклонов и антициклонов в атмосфере и других явлений. Обратимся к рассмотрению величины N
> 0. Это означает, что она направлена на запад, или, что то же, влево, если смотреть по направлению движения точки относительно земли. Соответственно материальная точка производит давление на связь вправо по отношению к направлению своей относительной скорости. Такое же положение сохраняется и при движении к югу. Можно показать (проделайте это!), что при движении точки по земной сфере по заданной криволинейной связи в северном полушарии материальная точка производит давление на связь вправо по направлению относительной скорости. Как известно, именно это обстоятельство лежит в основе объяснения подмыва реками своих правых берегов, образования циклонов и антициклонов в атмосфере и других явлений. Обратимся к рассмотрению величины N 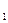 силы реакции связи. Нетрудно видеть, что эта сила характеризует вес материальной точки, движущейся по меридиану. Действительно весом следует называть, согласно изложенному выше, силу, с которой материальная точка давит на горизонтальную площадку (в данном случае силу, равную N
силы реакции связи. Нетрудно видеть, что эта сила характеризует вес материальной точки, движущейся по меридиану. Действительно весом следует называть, согласно изложенному выше, силу, с которой материальная точка давит на горизонтальную площадку (в данном случае силу, равную N 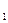 , но направленную противоположно). Точка почти теряет вес, если ее скорость по отношению к вращающейся Земле становится равной первой космической скорости:
, но направленную противоположно). Точка почти теряет вес, если ее скорость по отношению к вращающейся Земле становится равной первой космической скорости:
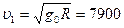
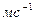 .
.
Как известно, обладая такой скоростью, спутник совершает вокруг Земли около семнадцати оборотов, двигаясь по окружности. При начальной скорости 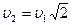 =11200
=11200 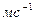 (вторая космическая скорость) спутник при отсутствии других небесных тел движется по параболе и навсегда удаляется от Земли.
(вторая космическая скорость) спутник при отсутствии других небесных тел движется по параболе и навсегда удаляется от Земли.
Пусть 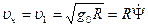 . Тогда
. Тогда 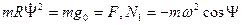 , что по модулю в 290 раз меньше силы тяготения на экваторе.
, что по модулю в 290 раз меньше силы тяготения на экваторе.
Рассмотрим условия равновесия материальной точки из меридиана. В этом случае в уравнениях (11) следует положить 
 .
.
Получим
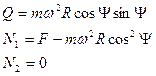 (14)
(14)
Первое уравнение (14) показывает, что на меридиане сферической Земли для равновесия необходимо к точке приложить силу, идущую по касательной к меридиану (всюду, кроме полюсов и ее экватора). Фактическая форма Земли не является сферой, и любое место на соответственно некруглом меридиане является положением равновесия точки. Необходимая для равновесия сила образуется за счет наличия неравной нулю проекции силы тяготения  на касательную меридиану, т.е. на направление истинного горизонта места, так как сила
на касательную меридиану, т.е. на направление истинного горизонта места, так как сила  немного отклонена от направления к центру Земли. При этом сумма векторов силы тяготения и переносной силы инерции
немного отклонена от направления к центру Земли. При этом сумма векторов силы тяготения и переносной силы инерции  направлена перпендикулярно плоскости истинного горизонта и образует так называемую силу тяжести. Из второго уравнения (14) следует, что величина
направлена перпендикулярно плоскости истинного горизонта и образует так называемую силу тяжести. Из второго уравнения (14) следует, что величина 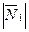 , или вес неподвижной материальной точки на сферической Земле достигает наибольшего значения на северном и южном полюсах, а наименьшего – на экваторе.
, или вес неподвижной материальной точки на сферической Земле достигает наибольшего значения на северном и южном полюсах, а наименьшего – на экваторе.

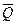 - сила, приложенная к рассматриваемой точке в направлении касательной к меридиану,
- сила, приложенная к рассматриваемой точке в направлении касательной к меридиану, 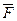 - сила тяготения точки к Земле,
- сила тяготения точки к Земле, 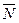 - реакция идеальной связи. Она расположена в плоскости, нормальной к меридиану, и ее можно разложить на две составляющие: вертикальную
- реакция идеальной связи. Она расположена в плоскости, нормальной к меридиану, и ее можно разложить на две составляющие: вертикальную  и горизонтальную
и горизонтальную 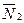 . Вертикальная составляющая при
. Вертикальная составляющая при 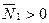 направлена по продолжению радиуса Земли вверх, а горизонтальная, если
направлена по продолжению радиуса Земли вверх, а горизонтальная, если 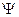 - геоцентрическая широта места. Отличие геоцентрической широты от географической (угол между той же плоскостью и истинной вертикалью места) – шесть дуговых минут на широте Парижа; R – радиус Земли;
- геоцентрическая широта места. Отличие геоцентрической широты от географической (угол между той же плоскостью и истинной вертикалью места) – шесть дуговых минут на широте Парижа; R – радиус Земли; 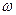 -угловая скорость Земли. За относительное движение примем перемещение точки по отношению к Земле, или, что то же, по отношению к географической сетке меридианов и параллелей, вращающейся вместе с Землей. Относительная скорость направлена по касательной к меридиану (рис. 5). Ее величина
-угловая скорость Земли. За относительное движение примем перемещение точки по отношению к Земле, или, что то же, по отношению к географической сетке меридианов и параллелей, вращающейся вместе с Землей. Относительная скорость направлена по касательной к меридиану (рис. 5). Ее величина 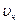 определяется формулой
определяется формулой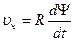 .
.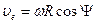 .
. состоит из двух составляющих: тангенциальной
состоит из двух составляющих: тангенциальной  и нормальной
и нормальной 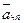 , соответственно направленных по касательной к меридиану и к центру Земли
, соответственно направленных по касательной к меридиану и к центру Земли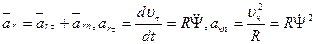 .
. . Переносное ускорение
. Переносное ускорение 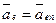 направлено к центру параллели (перпендикулярно оси Земли).
направлено к центру параллели (перпендикулярно оси Земли).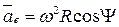


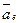 :
: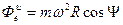 .
.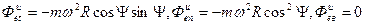 .
.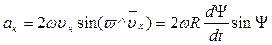 .
.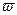 к вектору
к вектору 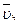 происходящим против хода часовой стрелки (Нетрудно проверить, что к тому же приводит правило Жуковского). Пусть
происходящим против хода часовой стрелки (Нетрудно проверить, что к тому же приводит правило Жуковского). Пусть  , тогда точка движется к северу, и ее кориолисово ускорение направленно на запад. Кориолисова сила инерции направлена на восток
, тогда точка движется к северу, и ее кориолисово ускорение направленно на запад. Кориолисова сила инерции направлена на восток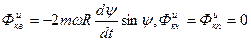 .
.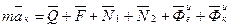 .
.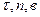 ), получим
), получим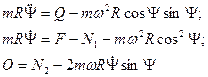 (11)
(11)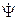 в начальный момент времени, можно найти широту
в начальный момент времени, можно найти широту  и N
и N  :
: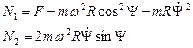
 ), то
), то  > 0. Это означает, что она направлена на запад, или, что то же, влево, если смотреть по направлению движения точки относительно земли. Соответственно материальная точка производит давление на связь вправо по отношению к направлению своей относительной скорости. Такое же положение сохраняется и при движении к югу. Можно показать (проделайте это!), что при движении точки по земной сфере по заданной криволинейной связи в северном полушарии материальная точка производит давление на связь вправо по направлению относительной скорости. Как известно, именно это обстоятельство лежит в основе объяснения подмыва реками своих правых берегов, образования циклонов и антициклонов в атмосфере и других явлений. Обратимся к рассмотрению величины N
> 0. Это означает, что она направлена на запад, или, что то же, влево, если смотреть по направлению движения точки относительно земли. Соответственно материальная точка производит давление на связь вправо по отношению к направлению своей относительной скорости. Такое же положение сохраняется и при движении к югу. Можно показать (проделайте это!), что при движении точки по земной сфере по заданной криволинейной связи в северном полушарии материальная точка производит давление на связь вправо по направлению относительной скорости. Как известно, именно это обстоятельство лежит в основе объяснения подмыва реками своих правых берегов, образования циклонов и антициклонов в атмосфере и других явлений. Обратимся к рассмотрению величины N 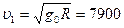
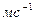 .
.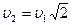 =11200
=11200 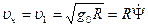 . Тогда
. Тогда 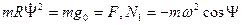 , что по модулю в 290 раз меньше силы тяготения на экваторе.
, что по модулю в 290 раз меньше силы тяготения на экваторе.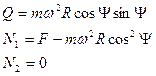 (14)
(14) на касательную меридиану, т.е. на направление истинного горизонта места, так как сила
на касательную меридиану, т.е. на направление истинного горизонта места, так как сила  направлена перпендикулярно плоскости истинного горизонта и образует так называемую силу тяжести. Из второго уравнения (14) следует, что величина
направлена перпендикулярно плоскости истинного горизонта и образует так называемую силу тяжести. Из второго уравнения (14) следует, что величина 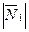 , или вес неподвижной материальной точки на сферической Земле достигает наибольшего значения на северном и южном полюсах, а наименьшего – на экваторе.
, или вес неподвижной материальной точки на сферической Земле достигает наибольшего значения на северном и южном полюсах, а наименьшего – на экваторе.


