Плоскость
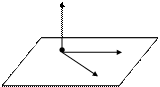
Вектором нормали к плоскости называется вектор, перпендикулярный к этой плоскости. Уравнение плоскости по точке
Рис. 12
имеет вид:
Это линейное уравнение относительно переменных
выражает плоскость, причем коэффициенты при переменных являются координатами вектора нормали
Пример 13. (Образец выполнения задачи 7(b) из контрольной работы). Найти уравнение плоскости, проходящей через точки
Рис. 13
т.к.
Запишем уравнение искомой плоскости по вектору нормали
Окончательно, после упрощений, имеем:
Полученный результат следует повторить, подставляя в уравнение координаты точек
Пример 14. (Образец выполнения задачи 7(c) из контрольной работы). Найти параметрические уравнения прямой, проходящей через точку
Решение. Т.к. искомая прямая перпендикулярна к плоскости, то ее направляющий вектор
Осталось лишь записать искомые уравнения прямой, используя формулы (2.4):
|

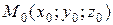 и заданному вектору нормали
и заданному вектору нормали 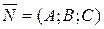 (рис. 12)
(рис. 12)




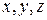 . Верно и обратное: всякое линейное уравнение
. Верно и обратное: всякое линейное уравнение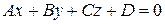
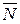 этой плоскости. Данное уравнение называется общим уравнением плоскости.
этой плоскости. Данное уравнение называется общим уравнением плоскости.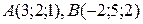 и
и 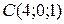 .
. Решение. Из точки
Решение. Из точки  выпустим два вектора
выпустим два вектора  и
и 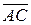 . Тогда в качестве нормали искомой плоскости можно взять векторное произведение векторов
. Тогда в качестве нормали искомой плоскости можно взять векторное произведение векторов 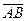 и
и 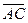 (рис. 13),
(рис. 13),
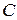
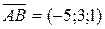 ,
, 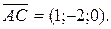
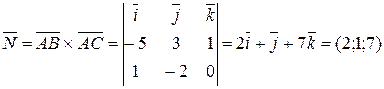 .
.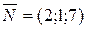 и, например, точке
и, например, точке 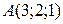 :
: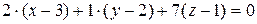 .
.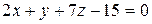 .
.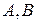 и
и 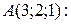
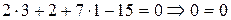 верно
верно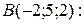
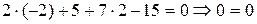 верно
верно
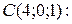
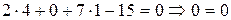 верно. n
верно. n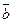 совпадет с вектором нормали плоскости
совпадет с вектором нормали плоскости 

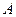
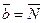



 Рис.14
Рис.14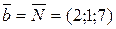 .
.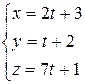 ,
, 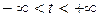 .n
.n


