Идентификация объекта автоматизации. Все расчеты здесь и далее произведены с помощью MAHTLAB и заимоствованы из курсовой работы Мироненко А

Все расчеты здесь и далее произведены с помощью MAHTLAB и заимоствованы из курсовой работы Мироненко А. В. «Автоматизация процесса сухого помола цементного клинкера в трубной шаровой мельнице»

Под идентификацией динамических объектов понимают процедуру определения структуры и параметров их математических моделей, которые при одинаковом входном сигнале объекта и модели обеспечивают близость выхода модели к выходу объекта при наличие какого-то критерия качества.

В результате проведенного эксперимента был получен массив данных состоящий из 2 тысяч значений входного параметра и 2 тысяч значений выходного параметра. Интервал дискретизации равен 3 с (ts=3). Для загрузки в рабочую область MATLAB массива данных необходимо выполнить команду:

После выполнения команды в рабочей области появились массив входных переменных u и массив выходного параметра y.

Интервал дискретизации указывается дополнительно:

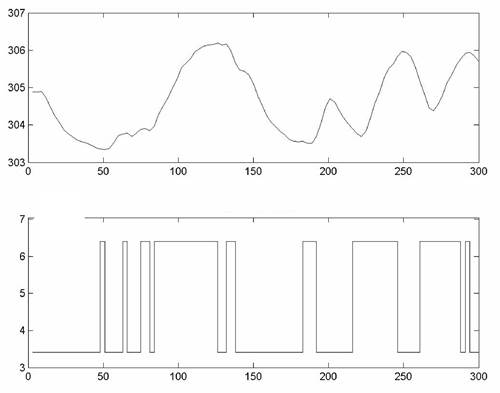
Сформированный файл указывает, что он содержит результаты 100 измерений с интервалом дискретизации 3 с. Входными переменными является массив u, а выходным параметром y. Для наглядности сформированного файла необходимо в его структуру ввести обозначения входных и выходных данных:

>>set(dan41,’InputName’,'Тонкоcть помола клинкера’,'OutputName’,'Влажноcть клинкера’)

Для просмотра полной информации о полученном файле воспользуемся командой:
>> get(dan41)

ans =

Domain: ‘Time’

Name: []

OutputData: [100×1 double]

y: [1×18 char]

OutputName: {[1×18 char]}

OutputUnit: {'’}

InputData: [100×1 double]

u: [1×17 char]

InputName: {[1×24 char]}

InputUnit: {'’}

Period: Inf

InterSample: ‘zoh’

Ts: 3

Tstart: []

SamplingInstants: [100×0 double]

TimeUnit: ‘’

ExperimentName: ‘Exp1′

Notes: []

UserData: []

Для графического представления данных воспользуемся командой:

plot(dan41) (рис.10):

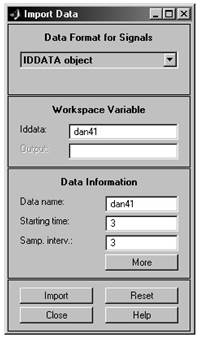
Для дальнейшего использования полученных исходных данных необходимо провести предварительную обработку этих данных с целью удаления тренда из набора данных и если необходимо отфильтровать данные с помощью имеющихся средств в пакете System Identification Toolbox. Данные операции проведем в графическом интерфейсе System Identification Toolbox, который запускается из командной строки командой:

>> ident

Opening ident ……. done.

Импортируем файл данных в среду интерфейса с помощью команды data – import (рис.11):

Запустим режим быстрого старта, для чего в падающем меню Operations выберем Quick Start. При выборе этого режима производится:

· удаление тренда из массива экспериментальных данных;

· формирование усеченных массивов данных с именами dande и dandv для построения моделей (рис. 12)

Тонкость помола и влажность клинкера

После проведения предварительной обработки данных можно приступить к нахождению оценки модели.

В предложенном списке Estimate выбираем Parametric models, данный выбор приведет к открытию диалогового окна задания структуры модели. Получим параметрические модели из предложенного списка (ARX, ARMAX, OE, BJ, State Space), оценка производится нажатием кнопки Estimate. Существует возможность изменить параметры модели в редакторе Order Editor.

Воспользуемся значениями по умолчанию, за исключением ARX и State Space, у которых параметры выберем, нажав кнопку Order Selection (рис.13).

Для анализа моделей воспользуемся средствами System Identification Toolbox: Model output, Transient resp, Frequency resp.

Для анализа модели ТОУ возьмем модель arx233 для чего перетащим ее на иконку To Workspace, при этом модель arx233 появится в рабочем пространстве MATLAB.

Полученные модели представлены в так называемом тета – формате и являются дискретными. Для преобразования модели из тета - формата в вид удобный для дальнейшего использования в пакете System Identification Toolbox имеются специальные функции.

Преобразуем модель тета-формата многомерного объекта в вектор передаточных функций, связанных с выбранным входом:

 

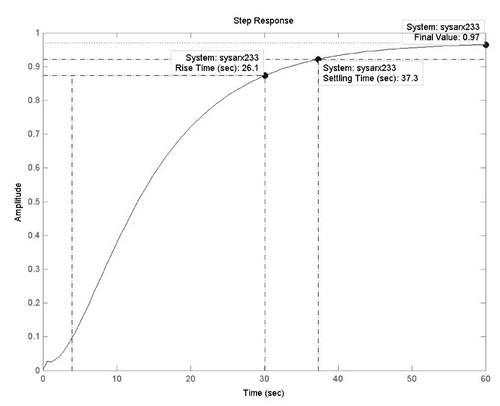
>> [A, B] =th2arx (arx233)
A =
1.0000 -1.2514 0.3763
B =
Columns 1 through 3
0 0 0
Columns 4 through 6
0.0600 0.0487 0.0125

>> [num,den]=th2tf(arx233)
num =
Columns 1 through 3
0 0 0
Columns 4 through 6
0.0600 0.0487 0.0125
den =
Columns 1 through 3
1.0000 -1.2514 0.3763
Columns 4 through 6
0 0 0

где num, den соответственно числитель и знаменатель дискретной передаточной функции.

Получим дискретную передаточную функцию:

>> zarx233 = tf(num, den, ts)

Transfer function:
0.05999 z^2 + 0.04869 z + 0.01253
———————————
z^5 - 1.251 z^4 + 0.3763 z^3

Sampling time: 3

Преобразуем дискретную модель в непрерывную и представим ее в виде передаточной функции:

>> sarx233 = thd2thc (arx233)
Continuous-time IDPOLY model: A(s) y (t) = B(s) u (t) + C(s) e (t)
A(s) = s^3 + 12.4 s^2 + 3.955 s + 0.2669
B(s) = 0.3928 s^2 - 0.1036 s + 0.2589
C(s) = s^3 + 12.8 s^2 + 8.952 s + 2.136
>> [num1, den1] =th2tf (sarx233)
num1 =
Columns 1 through 3
0 0.3928 -0.1036
Column 4
0.2589
den1 =
Columns 1 through 3
1.0000 12.3970 3.9546
Column 4
0.2669
>> sysarx233 = tf (num1, den1)
Transfer function:
0.3928 s^2 - 0.1036 s + 0.2589
———————————
s^3 + 12.4 s^2 + 3.955 s + 0.2669

Приведенные передаточные функции являются одной и той же моделью, записанной в разных формах и форматах. Проанализируем динамические характеристики модели. Для этого воспользуемся командой:

>> step(sysarx233) (рис. 14).

Рис. 14 Динамические характеристики модели

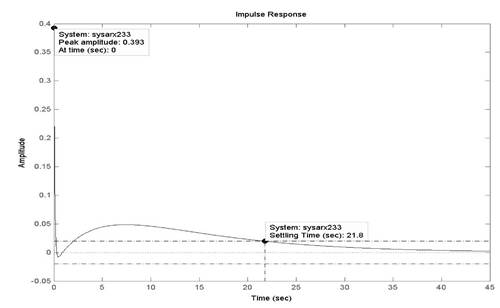
В поле графика указаны основные характеристики переходящего процесса: время нарастания, время регулирования, установившееся значение выходной координаты.

Для построения импульсной характеристики модели необходимо воспользоваться командой:

>> impulse(sysarx233) (рис. 15).

Рис. 15 Импульсная характеристика модели

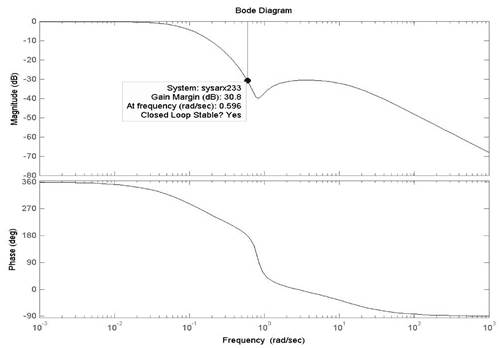
Определим частотные характеристики моделей с помощью команды: >> bode(sysarx233) (рис. 16).

Рис. 16 Частотные характеристики

Также можно просмотреть годограф Найквиста:

>> nyquist(sysarx233) (рис. 17).

Рис. 17 Годограф Найквиста (АФЧХ)

Найквиста годограф АФЧХ не пересекает точку комплексной плоскости с координатами -1,j0.

Значения запасов устойчивости можно определить также и в режиме командной строки MATLAB с помощью команды

 

>> [Gm, Pm, Wcg, Wcp] =margin (sysarx233)
Gm = 34.7465
Pm = Inf
Wcg = 0.5964
Wcp = NaN

где Gm – запас устойчивости по амплитуде в натуральных величинах на частоте Wcg, Pm – запас устойчивости по фазе на частоте Wcp. Для определения запасов устойчивости в логарифмическом масштабе необходимо выполнить следующие операции:

>> Gmlog=20•log10(Gm)
Gmlog = 30.8182

Как видно, определение запасов устойчивости последним способом позволяет значительно точнее вычислять эти значения, чем на графиках частотных характеристик.

Анализ частотных характеристик показывает, что модели arx233 являются устойчивыми с соответствующими запасами устойчивости по амплитуде. Запас устойчивости по фазе равен бесконечности.

Для решения задач анализа и синтеза систем управления важно знать ответ на другой не менее важный вопрос, чем полученные временные, частотные и статистические характеристики: обладает ли объект свойством управляемости в смысле возможности его перевода из заданной начальной точки (или области) в заданную конечную точку (или область)?

Решение проблемы управляемости основано на анализе уравнений переменных состояния и формулируется следующим образом: объект называется вполне управляемым, если выбором управляющего воздействия u(t) на интервале времени [t ₀ > t _k;] можно перевести его из любого начального состояния y(t_o) в произвольное заранее заданное конечное состояние y(t_k).

Критерием управляемости линейных стационарных объектов является условие: для того чтобы объект был, вполне управляем, необходимо и достаточно, чтобы ранг матрицы управляемости равнялся размерности вектора состояний п.

В пакете Control System Toolbox имеется функция ctrb, формирующая матрицу управляемости в пространстве состояний. Для того, чтобы воспользоваться этой функцией необходимо вычислить матрицы А, В, С, D с помощью команды:

>> [A, B, C, D] = ssdata (sysarx233)
A =
-12.3970 -0.9887 -0.0334
4.0000 0 0
0 2.0000 0
B =
0.5000
0
0
C = 0.7857 -0.0518 0.0647
D = 0
Вычислим матрицу управляемости:
>> Mu=ctrb (A, B)
Mu =
0.5000 -6.1985 74.8659
0 2.0000 -24.7941
0 0 4.0000
Определим ранг матрицы управляемости:
>> nMu=rank(Mu)
nMu = 3

При синтезе оптимальных систем с обратной связью сами управления получаются как функции от фазовых координат. В общем случае фазовые координаты являются абстрактными величинами и не могут быть исследованы. Поддается измерению (наблюдению) вектор у = (у₁, …,y_k)T, который обычно называют выходным вектором или выходной переменной, а его координаты - выходными величинами. Выходная переменная функционально связана с фазовыми координатами, и для реализации управления с обратной связью необходимо определить фазовые координаты по измеренным значениям выходной переменной. В связи с этим возникает проблема наблюдаемости, заключающаяся в установлении возможности состояния определения состояния объекта (фазового вектора) по измеренным значениям выходной переменной на некотором интервале.

Решение проблемы наблюдаемости основано на анализе уравнений переменных состояния и формулируется следующим образом: объект называется вполне наблюдаемым, если по реакции y(tk) на выходе объекта, на интервале времени [t₀, t_k] при заданном управляющем воздействии u(t) можно определить начальное состояние вектора переменных состояния x(t), являющихся фазовыми координатами объекта.

Критерием наблюдаемости линейных стационарных объектов является условие: для того, чтобы объект был вполне наблюдаемым, необходимо и достаточно, чтобы ранг матрицы наблюдаемости равнялся размерности вектора состояния п.

Определим матрицу наблюдаемости:

>> My=obsv (A, C)
My =
0.7857 -0.0518 0.0647
-9.9473 -0.6473 -0.0262
120.7278 9.7820 0.3318

Определим ранг матрицы наблюдаемости:

>> nMy=rank(My)
nMy = 3

Таким образом, для исследуемой модели объекта размерность вектора состояний, определяемая размером матриц A и C равна трем и ранг матрицы наблюдаемости MY также равен трем, что позволяет сделать вывод о том, что объект автоматизации является вполне наблюдаемым, т.е. для него всегда можно определить по, значениям выходной величины y(t) вектор переменных состояния, необходимый для синтеза системы управления. [1]