Задача 3. В условиях задачи 2 и договора с частичной защитой страховщик имеет однородный портфель из (220) аналогичных договоров
В условиях задачи 2 и договора с частичной защитой страховщик имеет однородный портфель из (220) аналогичных договоров. Найти: а) единовременную рисковую премию; б) относительную рисковую надбавку, обеспечивающую вероятность выполнения страховщиком своих обязательств не ниже (88) %,а также нетто-премию и брутто-премии, если нагрузка на ведение дел и прибыль составляет (21) % от тарифа; в) какими станут относительная рисковая надбавка, нетто- и брутто-премии, если объем портфеля увеличится в (13) раз. Решение: M(Y) = 137,385 у.е., D(Y)= 273808,9 у.е.2; σ(Y)=523,2676 у.е.; K(Y)=0,380877 n = 220 1 - e = 0,88 e = 1 - 0,88 = 0,12
Функция Лапласа Ф(t)=0,76 Þ по таблицам функции Лапласа нормального закона распределения: t = 1,17
Ф(t)=0,76 а) РП = M(Y) = 137,385 у.е. б) НП =РП∙(1+θ)= 137,385 ∙(1+0,030044)= 141,5126 у.е.
БП= В)
НП =РП∙(1+θ)=137,385∙(1+0, 0,008333)= 138,5298 у.е. БП= То есть с увеличением объема портфеля в 13 раз относительная рисковая надбавка уменьшится в
|
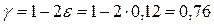
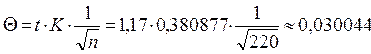
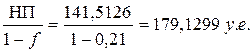
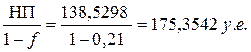
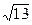раз, и соответственно уменьшатся и нетто- и брутто-премии, повысив, таким образом, конкурентоспособность страховщика.
