Задача 8.
Исследовать однородный страховой портфель объемом 5000 со страховой суммой: S=3000у.е., выплачиваемой полностью при наступлении страхового случая, вероятность которого: 0,002 Найти рисковую премию, нетто-премию, если надбавка должна обеспечить надежность не ниже: (71) %. Брутто-премию, если доля нагрузки в тарифе: (13) %. Какой резерв нужен страховщику, чтобы повысить надежность на 10 %? Оценить возможность перестрахования, если относительная надбавка у перестраховщика на треть больше, чем у страховщика, а Страхнадзор требует повысить надежность до (99) %. (Считать, что НП перестрахования оплачивается из СНП цедента.)
Так как p мало, используем для расчетов вероятностей формулу распределения Пуассона: Pn(k)= где λ=n∙p =5000∙0,002=10 - параметр распределения Пуассона; Pn(k) - вероятность того, что в портфеле из n договоров число страховых случаев будет равно k
Таким образом, можно утверждать, что с практической достоверностью > 0,999 в портфеле произойдет не более 21 страхового случая. а) Собранной с портфеля суммарной рисковой премии СРП= n∙p∙S =5000∙0,002∙3000=30000 у.е. будет достаточно для выплаты по 10 страховым случаям.Это обеспечивает вероятность выживания (см. таблицу) 0,583039750< 1-e =0,61, то есть надежность ниже заданной. Нужно рассчитать рисковую надбавку, чтобы иметь возможность покрыть не менее 12 страховых случаев, чтобы обеспечить рисковой надбавкой, заданную в условии надежность 71%. Для этого рисковая надбавка должна быть:
т.е. рисковая надбавка должна составлять 20% от рисковой премии. Таким образом, получаем премии на один договор: Рисковая премия: РП= p∙S =0,002∙3000=60 у.е; Нетто-премия: НП=РП∙(1+θ)=60∙1,2=72 у.е.; Брутто-премия:
Итак, мы получили, что собранная со всего портфеля рисковая премия покрывает только 10 страховых случая, но это намного меньше заданной надежности в 71% (только 61% надежности). За счет рисковой надбавки мы собираем со всего портфеля сумму для покрытия 12 страховых случаев. б) Если иметь резерв U в размере одной страховой суммы S=3000 у.е. для покрытия 13-го страхового случая, то надежность будет равна 86,4%, что явно больше основной надежности в 71% и даже превышает требуемую по условию надежность 81% (повышение надежности на 10%). в) Предположим, что страховая компания приняла решение удержать случаи до 13 включительно (обеспечивает выживание >86,4%), а на перестрахование передает 14 случай, чтобы обеспечить надежность > 91%. Если будет 14 страховых случаев, перестраховщик оплачивает один из них, выплачивает одну страховую сумму S = 3000 у.е. РПRe= M(Y Re ) = 3000∙ 0,315686= 947,0567 у.е. По условию рисковая надбавка перестраховщика:
Следовательно, его нетто- и брутто-премии составят:
|

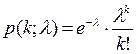 ,
,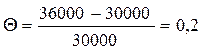 ,
, у.е.
у.е.






