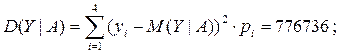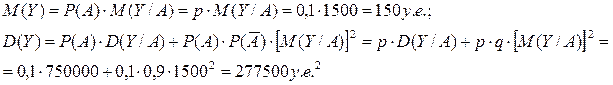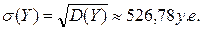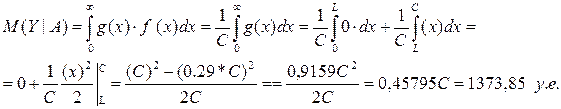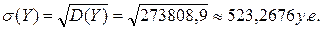Контрольная работа №2. Кафедра Математической статистики и эконометрики
Кафедра Математической статистики и эконометрики «Рисковое страхование» Выполнил: студент группы ДЭК-502 Цепов Алексей Проверила: к.т.н., доцент Миронкина Юлия Николаевна
Москва 2011 k=2 r=9
Задача 1.
Объектстоимостью 3тысяч у.е. застрахован, вероятность его повреждения оценена как р=0,1 При возникновении страхового случая вследствие конструктивных особенностей объекта величина ущерба распределена дискретно:
Найти характеристики ущерба страховщика (математическое ожидание и дисперсию выплат) для одного из предложенных страховщиком 5 возможных видов договоров согласно своему варианту: Г) безусловная франшиза (10 + 2) % от цены объекта
Решение:
Ответ: M(Y) = 112,8 у.е., D(Y) = 192188,2 у.е.
Задача 2. Имущество ценой 3тыс. у.е. застраховано от пожара сроком на 1 год. Вероятность страхового случая оценена в 10 %. При пожаре величина ущерба распределена равномерно от 0 до стоимости объекта 3тыс. у.е. Страховщик предложил 5 возможных вариантов договора: условная франшиза 29 % от цены объекта (вариант r=3 или 7 или 9). Сравнить договор с полной защитой (а) и договор с частичной защитой (по своему варианту).Проанализировать выбранные договора: найти характеристики размера ущерба страховщика (математическое ожидание, дисперсию, среднее квадратическое отклонение, коэффициент вариации).
Математическое ожидание договора с условной франшизой 29% от цены объекта при данных условиях обладает меньшим значением, чем договор с полной защитой. При этом договор с франшизой обладает меньшей степенью риска, об этом говорят значения дисперсии, среднего квадратического отклонения.
Задача 3
|