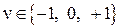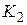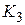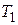АМПЛИТУДНО-ЧАСТОТНЫХ ХАРАКТЕРИСТИК СИСТЕМПередаточные функции
где В этом случае модули и аргументы передаточных функций системы
и звеньев
связаны между собой соотношениями:
Вещественные и мнимые частотные функции системы определяются равенствами:
Пользуясь полученными соотношениями можно построить АФЧХ. Логарифмическая амплитудная частотная характеристика для таких систем определяется выражением.
где Общее правило построения ЛЧХ (ЛАЧХ и ЛФЧХ) систем, передаточные функции которых преобразованы к виду (2.176): строят ЛЧХ отдельных звеньев и затем их графически складывают. Можно также сформулировать несколько иной, более простой порядок построения асимптотической ЛАЧХ: 1. Вычисляют сопрягающие частоты и значение 2. Строят первую асимптоту, которую проводят до первой сопрягающей частоты через точку с координатами 3. Проводят вторую асимптоту от конца первой асимптоты до второй сопрягающей частоты. Её наклон изменяется на 20, – 20, 40 или – 40 дБ/дек в зависимости от того, является ли 4. Строят каждую последующую асимптоту аналогично второй. Изменение наклона Если какая-либо сопрягающая частота является кратной и её кратность равна Пример 2.18. Для системы, описываемой передаточной функцией
постройте асимптотическую логарифмическую амплитудно–частотную характеристику. Параметры передаточной функции Таблица 2.4
|
разомкнутых систем управления легко могут быть преобразованы к виду:
, (2.176)
– передаточные функции типовых или элементарных звеньев.
, 
, 
, 
.
, 
.
,
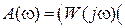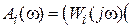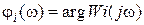
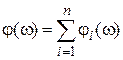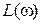и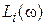 
– логарифмические амплитудные частотные функции системы и звеньев, входящих в систему.
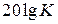, где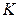 
- статический коэффициент передачи системы, равный произведению статических коэффициентов передачи звеньев 
.
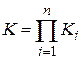и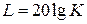 
с наклоном 
дБ/дек. Здесь 
равно разности между числами интегрирующих и дифференцирующих звеньев.
сопрягающей частотой форсирующего, апериодического, форсирующего второго порядка или колебательного звена соответственно.
– й асимптоты зависит от того, сопрягающей частотой какого элементарного звена является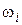 
.
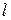, т.е. имеется 
; 
; 
