Задача 6.2. Если данную линию разбить на элементарные части (малые дуги) и считать приближенно каждую часть однородной
Если данную линию разбить на элементарные части (малые дуги) и считать приближенно каждую часть однородной, то бесконечно малый элемент массы будет равен
По условию задачи составляем формулу для плотности в точке
Тогда
Вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла по некоторой независимой переменной (параметру), через которую выражаются переменные
(использована формула для дифференциала длины дуги в полярных координатах). Тогда Ответ к задаче 6.2:
|
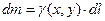, где 
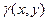- это линейная плотность распределения массы.
: 
.
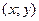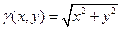,где 
- это окружность 
.
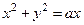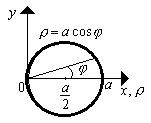Теперь будем вычислять составленный криволинейный интеграл первого рода по окружности, уравнение которой проще записать в полярных координатах, учитывая что 
:
.
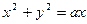
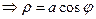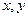и дифференциал длины дуги 
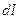. Выберем такой независимой переменной полярный угол 
, изменяющийся на линии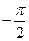 
до 
, и выразим через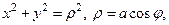 
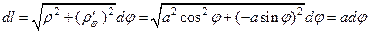
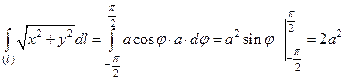
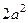(ед. массы).
