Задача 8.1
Векторное поле
, (оператор Гамильтона). При этом функция
Необходимым и достаточным условием потенциальности поля односвязной области, является равенство нулю его ротора:
Поэтому для проверки потенциальности данного поля вычислим его ротор: для данного поля поэтому
следовательно, данное векторное поле является потенциальным.
Для данного поля получим
Далее восстанавливаем функцию
=
Проверка:
В ответе учтем, что потенциал векторного поля находится с точностью до постоянного слагаемого С.
Ответ к задаче 8.1:
|
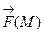, где 
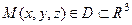, называется потенциальным, если оно является градиентом некоторого скалярного поля 
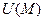, т.е..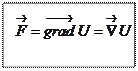
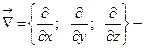векторный дифференциальный оператор «набла»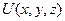
называется потенциалом векторного поля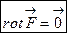 
.
;
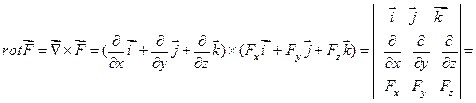
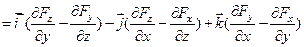его проекции равны: 
, 
, 
,
,
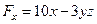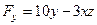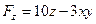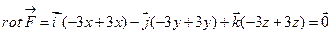Для нахождения потенциала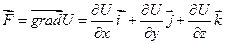 
, поэтому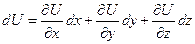
.
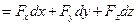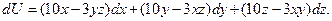
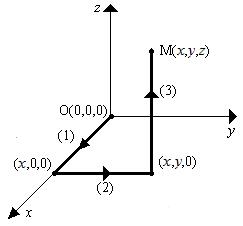
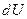интегрированием от некоторой фиксированной точки, например, 
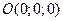до переменной точки 
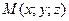по ломаной, состоящей из отрезков, параллельных осям координат: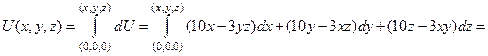
=
.
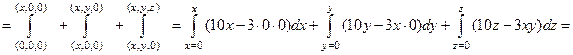
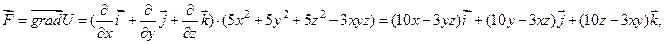что совпадает с данным вектором 
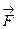в условии задачи, следовательно, функция 
.
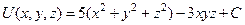