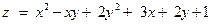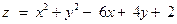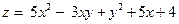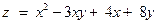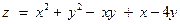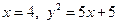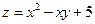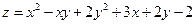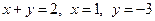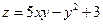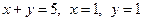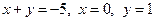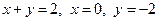Циркуляцией вектора  по замкнутому контуру
по замкнутому контуру  называется криволинейный интеграл II рода от скалярного произведения вектора
называется криволинейный интеграл II рода от скалярного произведения вектора  на вектор бесконечно малого перемещения
на вектор бесконечно малого перемещения 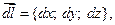 то есть
то есть
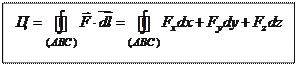
На контуре  выберем обход против часовой стрелки, поскольку иное не оговорено в условии задачи.
выберем обход против часовой стрелки, поскольку иное не оговорено в условии задачи.
В данной задаче  поэтому
поэтому
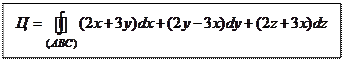 .
.
Используя свойство аддитивности криволинейного интеграла, будем вычислять интеграл по замкнутой ломаной как сумму интегралов по её частям.

Сводим каждый криволинейный интеграл к определенному интегралу:
на участке 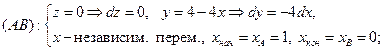
уравнение 
уравнение 

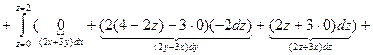
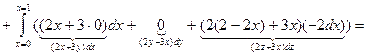
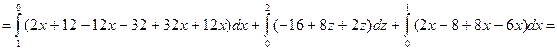


– это значение циркуляции по
контуру 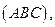 вычисленное непосредственно.
вычисленное непосредственно.
По формуле Стокса:
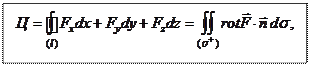
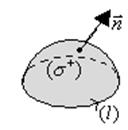
где  - это поверхность, опирающаяся на контур (l),
- это поверхность, опирающаяся на контур (l),
 - единичный вектор нормали к поверхности, направленный так, чтобы с его конца обход по контуру был виден против часовой стрелки.
- единичный вектор нормали к поверхности, направленный так, чтобы с его конца обход по контуру был виден против часовой стрелки.
Вычислим
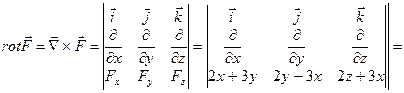
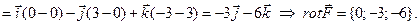
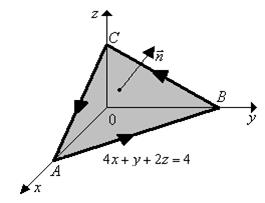 В качестве поверхности
В качестве поверхности  , опирающейся на контур
, опирающейся на контур  , можно выбрать плоскость треугольника с единичным вектором нормали
, можно выбрать плоскость треугольника с единичным вектором нормали 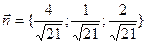
(вычислялся в задаче 8.2).. Поэтому 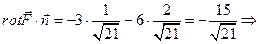
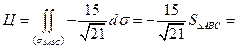
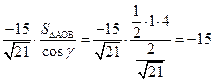 - это значение искомой циркуляции, вычисленное по формуле Стокса и, естественно, совпадающее со значением, вычисленным непосредственно.
- это значение искомой циркуляции, вычисленное по формуле Стокса и, естественно, совпадающее со значением, вычисленным непосредственно.
Отрицательное значение циркуляции указывает на то, что под действием данного векторного поля фактическое движение по контуру (ABC) будет осуществляться в противоположном направлении – по часовой стрелке.
Ответ к задаче 8.3: 
Варианты всех задач
Задание 1
Найти наибольшее и наименьшее значения функции 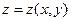 в замкнутой области D, ограниченной заданными линиями. Результаты решения вынести на чертеж области D.
в замкнутой области D, ограниченной заданными линиями. Результаты решения вынести на чертеж области D.
| № варианта
| Функция 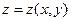
| Уравнения границ обл.D
|
|
| 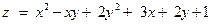
| x = 0, y = 0, x + y = –5
|
|
| 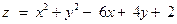
| x = 1, y = –3, x + y = 2
|
|
| 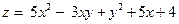
| x = –1, y = –2, x + y = 1
|
|
| 
| x = –1, y = 0, x + y = 3
|
|
| 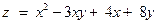
| x = 0, y =4, x + y = –2
|
|
| 
| x = –1, y = –1, y + x = 5
|
|
| 
| x = – 3, y = – 1, x + y = 0
|
|
| 
| x = –1, y = 2, x – y = 0
|
|
| 
| x = 0, y = 0, x + y = 4
|
|
| 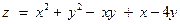
| x = 1, y = 3, x + y = –3
|
|
| 
| 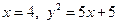
|
|
| 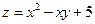
| 
|
|
| 
| 
|
|
| 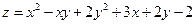
| 
|
|
| 
| 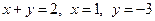
|
|
| 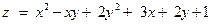
| x = 1, y = 0, x + y = –4
|
|
| 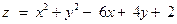
| x = 2, y = –4, x + y = 2
|
|
| 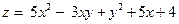
| x = –2, y = –1, x + y = 1
|
|
| 
| x = –3, y = -1, x + y = 3
|
|
| 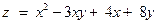
| x = 0, y =2, x + y = –2
|
|
| 
| x = –1, y = 0, y + x = 5
|
|
| 
| x = 3, y = – 1, x - y = 0
|
|
| 
| x = –2, y = 2, x+ y = 0
|
|
| 
| x = 1, y = 1, x + y = 4
|
|
| 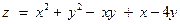
| x = 3, y = 1, x + y = –3
|
|
| 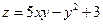
| 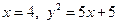
|
|
| 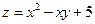
| 
|
|
| 
| 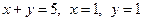
|
|
| 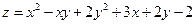
| 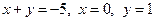
|
|
| 
| 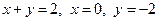
|

 – это значение циркуляции по
– это значение циркуляции по


 по замкнутому контуру
по замкнутому контуру  называется криволинейный интеграл II рода от скалярного произведения вектора
называется криволинейный интеграл II рода от скалярного произведения вектора 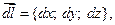 то есть
то есть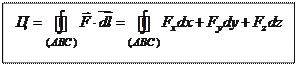
 поэтому
поэтому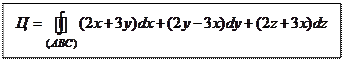 .
.
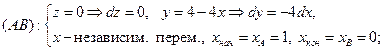



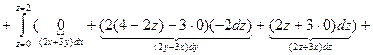
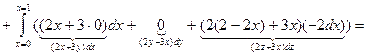
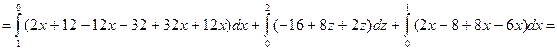
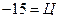
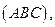 вычисленное непосредственно.
вычисленное непосредственно.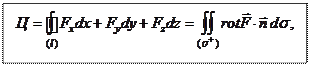

 - это поверхность, опирающаяся на контур (l),
- это поверхность, опирающаяся на контур (l), - единичный вектор нормали к поверхности, направленный так, чтобы с его конца обход по контуру был виден против часовой стрелки.
- единичный вектор нормали к поверхности, направленный так, чтобы с его конца обход по контуру был виден против часовой стрелки.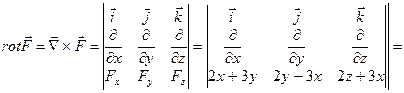
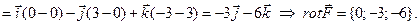
 В качестве поверхности
В качестве поверхности  , опирающейся на контур
, опирающейся на контур  , можно выбрать плоскость треугольника с единичным вектором нормали
, можно выбрать плоскость треугольника с единичным вектором нормали 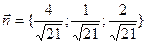
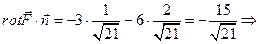
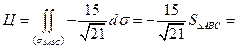
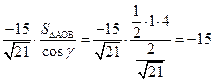 - это значение искомой циркуляции, вычисленное по формуле Стокса и, естественно, совпадающее со значением, вычисленным непосредственно.
- это значение искомой циркуляции, вычисленное по формуле Стокса и, естественно, совпадающее со значением, вычисленным непосредственно.
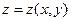 в замкнутой области D, ограниченной заданными линиями. Результаты решения вынести на чертеж области D.
в замкнутой области D, ограниченной заданными линиями. Результаты решения вынести на чертеж области D.