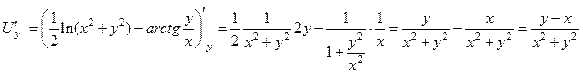Задача 6.3Проверяем необходимое и достаточное условие полного дифференциала функции двух переменных:
В данной задаче: условие полного дифференциала выполнено, следовательно, восстановить функцию Для нахождения функции
Так как криволинейный интеграл от полного дифференциала не зависит от формы линии интегрирования, то будем его вычислять по ломаной
Запишем уравнения каждого звена ломаной и, используя свойство аддитивности криволинейного интеграла, будем сводить его вычисление к вычислению определенных интегралов:
уравнение уравнение
Таким образом, искомая функция получилась в виде:
Проверка:
вычисленный полный дифференциал dU совпадает с данным в условии задачи, следовательно, функция
В записи ответа учтем, что функция нескольких переменных восстанавливается по её полному дифференциалу с точностью до постоянного слагаемого.
|
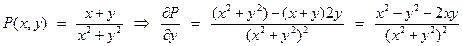
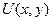можно.
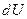по линии 
, соединяющей фиксированную точку 
и переменную точку 
в области существования криволинейного интеграла:
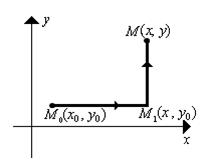
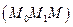, состоящей из отрезков, параллельных осям координат.
: 
: 
.
.
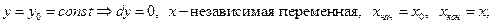
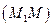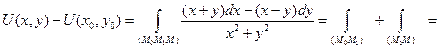
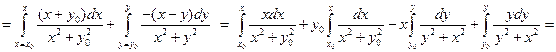
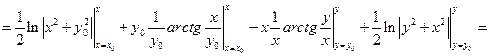
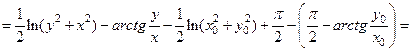
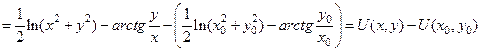