
|
Определим вид каждой поверхности:
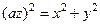 - это уравнение конуса, - это уравнение конуса,
 - это уравнение сферы радиуса - это уравнение сферы радиуса
 с центром в начале координат.
Строим искомый объем пересечением данных поверхностей и записываем формулу для его вычисления с помощью тройного интеграла: с центром в начале координат.
Строим искомый объем пересечением данных поверхностей и записываем формулу для его вычисления с помощью тройного интеграла:
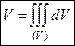 . .
|
Проще всего вычислить тройной интеграл по такому объему в сферических координатах, в которых объем (V) записывается следующей системой неравенств:

Переводим тройной интеграл к сферическим координатам и вычисляем его сведением к трехкратному интегралу:


Замечания к решению:

| 1)в упрощении выражения 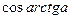 использовался прямоугольный треугольник, в котором использовался прямоугольный треугольник, в котором
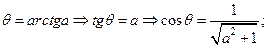 2) в вычислении трехкратного повторного интеграла использовано то, что внутренний интеграл вычисляется от такой функции и в таких пределах, которые не зависят от переменных внешних интегралов. Поэтому повторный интеграл в таком случае равен просто произведению интегралов.
2) в вычислении трехкратного повторного интеграла использовано то, что внутренний интеграл вычисляется от такой функции и в таких пределах, которые не зависят от переменных внешних интегралов. Поэтому повторный интеграл в таком случае равен просто произведению интегралов.
|
Ответ к задаче 5.1: 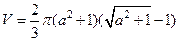 (ед. объема).
(ед. объема).


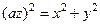 - это уравнение конуса,
- это уравнение конуса,
 - это уравнение сферы радиуса
- это уравнение сферы радиуса
 с центром в начале координат.
Строим искомый объем пересечением данных поверхностей и записываем формулу для его вычисления с помощью тройного интеграла:
с центром в начале координат.
Строим искомый объем пересечением данных поверхностей и записываем формулу для его вычисления с помощью тройного интеграла:
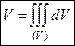 .
.




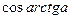 использовался прямоугольный треугольник, в котором
использовался прямоугольный треугольник, в котором
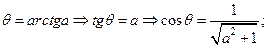 2) в вычислении трехкратного повторного интеграла использовано то, что внутренний интеграл вычисляется от такой функции и в таких пределах, которые не зависят от переменных внешних интегралов. Поэтому повторный интеграл в таком случае равен просто произведению интегралов.
2) в вычислении трехкратного повторного интеграла использовано то, что внутренний интеграл вычисляется от такой функции и в таких пределах, которые не зависят от переменных внешних интегралов. Поэтому повторный интеграл в таком случае равен просто произведению интегралов.
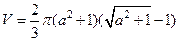 (ед. объема).
(ед. объема).


