Данный повторный интеграл мог получиться как результат вычисления двойного интеграла от функции 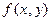 по области
по области 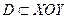 , записанной системой следующих неравенств:
, записанной системой следующих неравенств: 
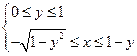 .
.
Поэтому для решения задачи нужно построить область 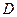 , записать ее неравенствами другим способом (т.е. первое неравенство должно быть по
, записать ее неравенствами другим способом (т.е. первое неравенство должно быть по 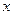 в постоянных пределах, а второе – по
в постоянных пределах, а второе – по  в пределах, зависящих от
в пределах, зависящих от 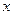 ), а затем двойной интеграл вновь свести к повторному в соответствии с другой системой неравенств. Этими действиями и изменится порядок интегрирования в данном повторном интеграле.
), а затем двойной интеграл вновь свести к повторному в соответствии с другой системой неравенств. Этими действиями и изменится порядок интегрирования в данном повторном интеграле.

 - нижняя граница области
- нижняя граница области 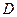 ,
,
 - верхняя граница,
- верхняя граница,
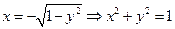 - левая граница,
- левая граница,
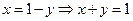 - правая граница;
- правая граница;
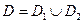 ;
;


Тогда

 =
= 
Ответ: 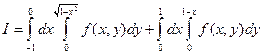 .
.

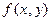 по области
по области 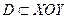 , записанной системой следующих неравенств:
, записанной системой следующих неравенств: 
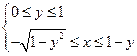 .
.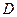 , записать ее неравенствами другим способом (т.е. первое неравенство должно быть по
, записать ее неравенствами другим способом (т.е. первое неравенство должно быть по 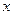 в постоянных пределах, а второе – по
в постоянных пределах, а второе – по  в пределах, зависящих от
в пределах, зависящих от 
 - нижняя граница области
- нижняя граница области  - верхняя граница,
- верхняя граница,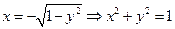 - левая граница,
- левая граница,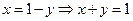 - правая граница;
- правая граница;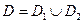 ;
;


 =
= 
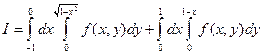 .
.


