1) Линией уровня скалярного поля  называется линия, в каждой точке которой функция
называется линия, в каждой точке которой функция 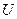 имеет постоянное значение.
имеет постоянное значение.
 Для данного скалярного поля
Для данного скалярного поля  уравнения линий уровня имеют вид
уравнения линий уровня имеют вид 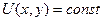



 ; здесь постоянная
; здесь постоянная 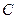 равна значению функции
равна значению функции 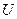 в точке
в точке 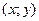 , через которую проходит линия уровня. Семейство линий уровня представляет собой множество парабол с вершинами в точках
, через которую проходит линия уровня. Семейство линий уровня представляет собой множество парабол с вершинами в точках  и ветвями, направленными вверх.
и ветвями, направленными вверх.
если  , то имеем линию уровня
, то имеем линию уровня  , на которой
, на которой 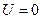 ;
;
если  , то имеем линию уровня
, то имеем линию уровня 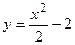 , на которой
, на которой  ;
;
если 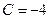 , то имеем линию уровня
, то имеем линию уровня  , на которой
, на которой  .
.
Находим градиент данного скалярного поля:


 ;
;
смысл этого вектора состоит в том, что в каждой точке 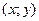 он показывает направление, в котором функция
он показывает направление, в котором функция  возрастает с наибольшей скоростью.
возрастает с наибольшей скоростью.
2) В фиксированной точке  :
:


 ;
;
 , где
, где  - это орт направления
- это орт направления  ;
;
Направляющие косинусы вектора  вычисляем по известным формулам геометрии:
вычисляем по известным формулам геометрии:
 ,
,  ,
, 
 если
если 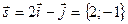 , то
, то  ,
,  ,
,  ;
;
 ,
,  ;
;

 - это значение указывает на то, что в точке
- это значение указывает на то, что в точке 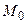 в направлении вектора
в направлении вектора  данная функция
данная функция  возрастает со скоростью, величина которой
возрастает со скоростью, величина которой  ;
;
скорость наибольшего возрастания функции  в той же точке
в той же точке 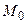 - это скорость ее изменения в направлении вектора градиента, величина этой скорости равна модулю вектора градиента:
- это скорость ее изменения в направлении вектора градиента, величина этой скорости равна модулю вектора градиента:

 =
= 
 .
.
3) Выполним построение в точке 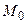 линии уровня вектора градиента:
линии уровня вектора градиента:

 уравнение линии уровня:
уравнение линии уровня: 
 ;
;
вектор  имеет направление, перпендикулярное к линии уровня, проходящей через точку
имеет направление, перпендикулярное к линии уровня, проходящей через точку 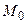 .
.
Ответ: 1) линии уровня  ,
,  ;
;
2)  ,
,  ,
,
величина скорости наибольшего возрастания функции U в точке 
равна  .
.

 называется линия, в каждой точке которой функция
называется линия, в каждой точке которой функция 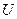 имеет постоянное значение.
имеет постоянное значение. Для данного скалярного поля
Для данного скалярного поля  уравнения линий уровня имеют вид
уравнения линий уровня имеют вид 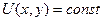



 ; здесь постоянная
; здесь постоянная 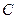 равна значению функции
равна значению функции 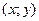 , через которую проходит линия уровня. Семейство линий уровня представляет собой множество парабол с вершинами в точках
, через которую проходит линия уровня. Семейство линий уровня представляет собой множество парабол с вершинами в точках  и ветвями, направленными вверх.
и ветвями, направленными вверх. , то имеем линию уровня
, то имеем линию уровня  , на которой
, на которой 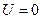 ;
; , то имеем линию уровня
, то имеем линию уровня 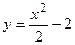 , на которой
, на которой  ;
;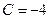 , то имеем линию уровня
, то имеем линию уровня  , на которой
, на которой  .
.
 ;
; :
:

 ;
; , где
, где  - это орт направления
- это орт направления  ;
; ,
,  ,
, 
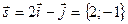 , то
, то  ,
,  ,
,  ;
; ,
,  ;
;
 - это значение указывает на то, что в точке
- это значение указывает на то, что в точке 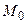 в направлении вектора
в направлении вектора  ;
;
 =
= 
 .
.

 ;
; имеет направление, перпендикулярное к линии уровня, проходящей через точку
имеет направление, перпендикулярное к линии уровня, проходящей через точку  ,
,  ;
; ,
,  ,
,
 .
.


