Задача 4.3
Если пренебречь изменением плотности материала в пределах элементарной площадки, то где
Тогда Это и есть формула для вычисления искомого момента инерции.
Вычисление записанного двойного интеграла удобно провести в полярной системе координат, в которой Тогда
Ответ к задаче 4.3:
|
Разбив данную фигуру на элементарные части, запишем бесконечно малый элемент искомого момента инерции, заменяя элементарную площадку материальной точкой 
с массой 
:
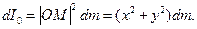
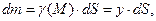
(по условию задачи),
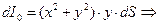
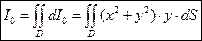
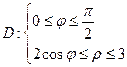- это площадь элементарной части.
и 
.
.
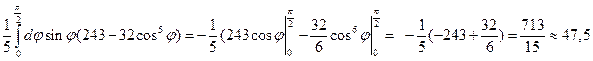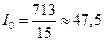(ед. момента инерции).
