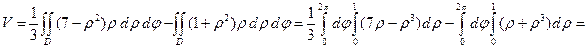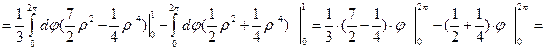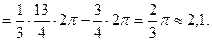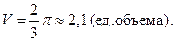Задача 4.2
Данное тело ограничено двумя параболоидами. Решая систему их уравнений
Строим каждую поверхность в отдельности, а затем выделяем объем, получающийся пересечением построенных поверхностей:
Искомый объем равен разности объемов двух цилиндроидов с одним основанием (круг
Тогда формула для вычисления искомого объема имеет вид:
Для вычисления составленных двойных интегралов область Переходя к полярным координатам в двойных интегралах, находим, что
Ответ к задаче 4.2:
|
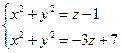, находим уравнение линии пересечения параболоидов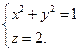 
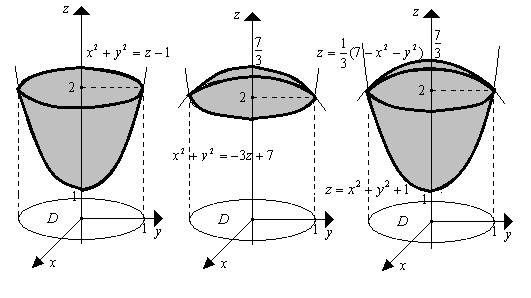
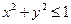) и ограниченных сверху соответственно поверхностям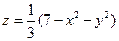и 
и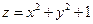 
. Поэтому можно использовать формулу для вычисления объема цилиндроида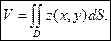
.
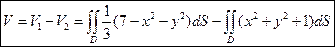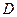удобно записать неравенствами в полярных координатах: 
.
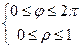