1. Описание теоретического решения задачи
Существование решения поставленной задачи гарантируется одним из свойств непрерывных функций: если ФНП является непрерывной на замкнутой области, то она достигает своих наибольшего и наименьшего значений на этой области.
Данная функция двух переменных 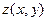 является непрерывной в замкнутой области, поэтому ее наибольшее и наименьшее значения в этой области существуют:
является непрерывной в замкнутой области, поэтому ее наибольшее и наименьшее значения в этой области существуют:
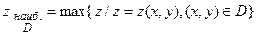 ,
,
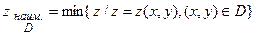 .
.
Эти значения называют глобальными экстремумами функции 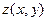 в области D, они могут достигаться либо в точках локальных экстремумов, лежащих внутри области D, либо на границе области D.
в области D, они могут достигаться либо в точках локальных экстремумов, лежащих внутри области D, либо на границе области D.
Для наглядности процесса практического решения задачи нужно построить область D в системе координат и отмечать в ее точках значения функции z, которые далее будут
вычисляться:

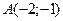 ,
, 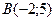 ,
, 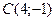
уравнение
AB:
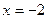
уравнение AC: 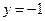
уравнение BC: 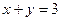
2. Нахождение локальных экстремумов функции z(x,y) внутри области D
Используем необходимые и достаточные условия для точки локального экстремума ФНП 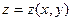 .
.
Необходимые условия: 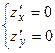

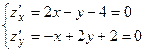

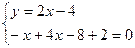

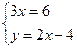

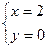

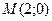 - это стационарная точка (подозрительная на экстремум), она является внутренней для области D.
- это стационарная точка (подозрительная на экстремум), она является внутренней для области D.
Достаточное условие экстремума:
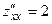 ,
, 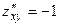 ,
, 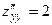

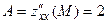 ,
, 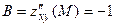 ,
, 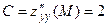

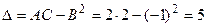
 в стационарной точке M есть экстремум, так как
в стационарной точке M есть экстремум, так как 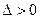 , причем минимум, так как
, причем минимум, так как 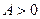 . Вычисляем значение функции z в точке минимума:
. Вычисляем значение функции z в точке минимума:
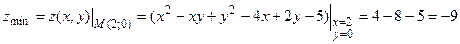 ;
;
Выносим это значение z на область D в точку 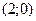 .
.
3. Исследование значений функции z(x,y) на границе области D
Так как в решаемой задаче граница области D является кусочно-заданной, то нужно исследовать функцию 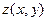 на каждом участке границы в отдельности.
на каждом участке границы в отдельности.
На участке AB: 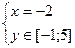

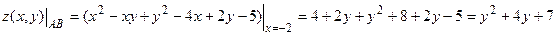
 на участке границы функция двух переменных
на участке границы функция двух переменных 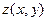 заменилась функцией одной переменной
заменилась функцией одной переменной 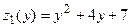 ,
, 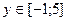 ;
;
Ее наибольшее и наименьшее значение на замкнутом промежутке можно найти, построив схематично график на этом промежутке:
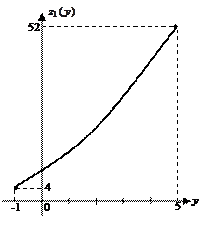
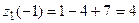 ,
,
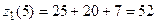 ;
;
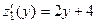

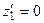 при
при 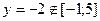

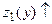 ;
;
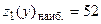 при
при 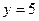 ,
,
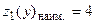 при
при 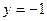 ;
;
Переносим результаты исследования функции 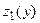 на функцию
на функцию 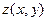 : на участке
: на участке 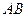 получим, что
получим, что 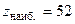 - достигается в точке
- достигается в точке 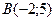 ,
, 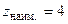 - достигается в точке
- достигается в точке 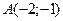 ; выносим эти значения на чертеж области
; выносим эти значения на чертеж области 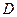 .
.
На участке AC: 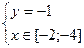

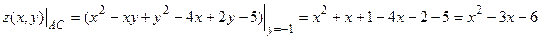
 обозначим
обозначим 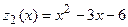 ,
, 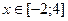 и построим схематично график:
и построим схематично график:

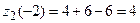 ,
,
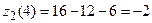 ;
;
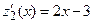

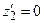 при
при 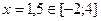

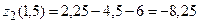 ;
;
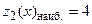 при
при 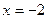 ,
,
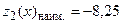 при x=1,5;
при x=1,5;
На участке 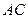 получим, что
получим, что 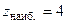 - достигается в точке
- достигается в точке 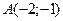 ,
, 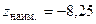 - достигается в точке
- достигается в точке 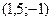 ; выносим эти значения также на чертеж области
; выносим эти значения также на чертеж области  .
.
На участке BC: 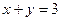

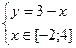

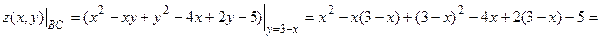
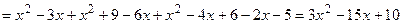
 обозначим
обозначим 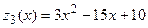 ,
, 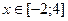 и построим схематично график:
и построим схематично график:
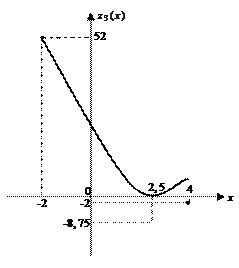
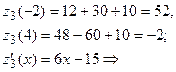
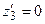 при
при 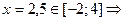
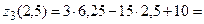
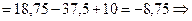
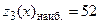 при
при 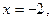
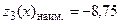 при
при 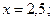
На участке 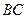 получим, что
получим, что 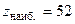 - достигается в точке
- достигается в точке 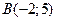 ,
, 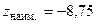 - достигается в точке
- достигается в точке 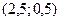 ; выносим эти значения так же на чертеж области
; выносим эти значения так же на чертеж области 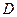 , контролируя при этом в угловых точках
, контролируя при этом в угловых точках 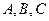 совпадение значений функции
совпадение значений функции 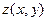 , которые получились на разных участках границы области
, которые получились на разных участках границы области 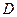 .
.
4. Получение ответа
Сравнивая между собой все значения функции 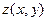 , которые были найдены в решении задачи и вынесены на чертеж области
, которые были найдены в решении задачи и вынесены на чертеж области 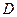 , выбираем из них наибольшее и наименьшее и составляем ответ.
, выбираем из них наибольшее и наименьшее и составляем ответ.
Ответ: 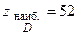 - достигается в точке
- достигается в точке 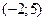 ,
, 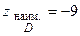 - достигается в точке
- достигается в точке 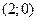 .
.
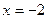

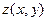 является непрерывной в замкнутой области, поэтому ее наибольшее и наименьшее значения в этой области существуют:
является непрерывной в замкнутой области, поэтому ее наибольшее и наименьшее значения в этой области существуют: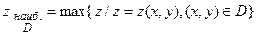 ,
,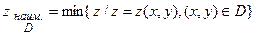 .
.
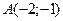 ,
, 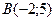 ,
, 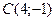
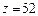
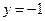
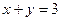
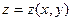 .
.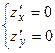

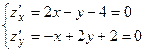

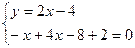
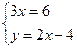
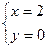
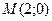 - это стационарная точка (подозрительная на экстремум), она является внутренней для области D.
- это стационарная точка (подозрительная на экстремум), она является внутренней для области D.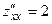 ,
, 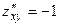 ,
, 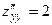
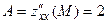 ,
, 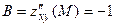 ,
, 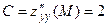
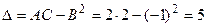
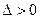 , причем минимум, так как
, причем минимум, так как 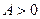 . Вычисляем значение функции z в точке минимума:
. Вычисляем значение функции z в точке минимума: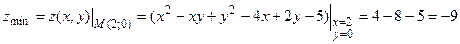 ;
;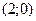 .
.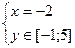
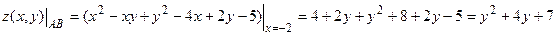
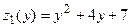 ,
,  ;
;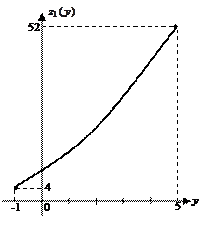
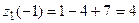 ,
,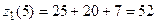 ;
;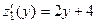
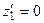 при
при 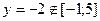
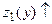 ;
;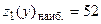 при
при 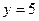 ,
,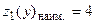 при
при 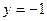 ;
;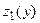 на функцию
на функцию 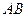 получим, что
получим, что 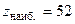 - достигается в точке
- достигается в точке 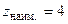 - достигается в точке
- достигается в точке  .
.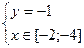
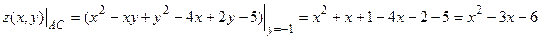
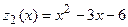 ,
, 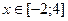 и построим схематично график:
и построим схематично график:
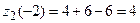 ,
,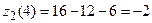 ;
;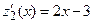
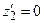 при
при 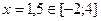
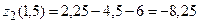 ;
;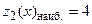 при
при 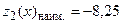 при x=1,5;
при x=1,5; получим, что
получим, что 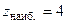 - достигается в точке
- достигается в точке 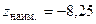 - достигается в точке
- достигается в точке 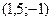 ; выносим эти значения также на чертеж области
; выносим эти значения также на чертеж области 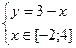
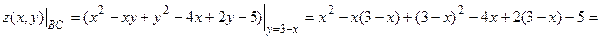
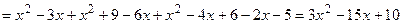
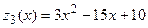 ,
, 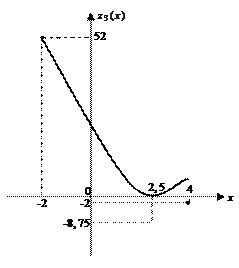
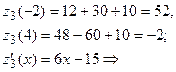
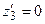 при
при 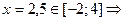
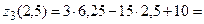
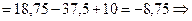
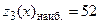 при
при 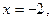
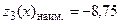 при
при 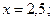
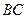 получим, что
получим, что 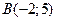 ,
, 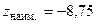 - достигается в точке
- достигается в точке 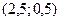 ; выносим эти значения так же на чертеж области
; выносим эти значения так же на чертеж области  совпадение значений функции
совпадение значений функции 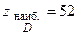 - достигается в точке
- достигается в точке 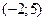 ,
, 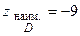 - достигается в точке
- достигается в точке 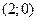 .
.


