Задача 4.1
1)
2)
проходит через точки
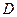 , с помощью двойного интеграла вычисляется по формуле:
Записав область сводим двойной интеграл к повторному и вычисляем его:
Ответ к задаче 4.1:
|
Задача 4.1
1)
2)
проходит через точки
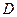, с помощью двойного интеграла вычисляется по формуле:
Записав область сводим двойной интеграл к повторному и вычисляем его:
Ответ к задаче 4.1:
|
Строим область 
– окружность с центром в т. (0; 1) и 
;
– парабола с вершиной в точке 
, имеет горизонтальную ось симметрии,
и 
.
= 
(ед. площади).
