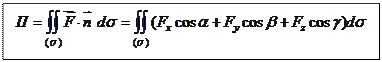 Потоком векторного поля
Потоком векторного поля  через двухстороннюю поверхность
через двухстороннюю поверхность  в направлении ее нормали
в направлении ее нормали 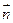 называется поверхностный интеграл по поверхности
называется поверхностный интеграл по поверхности  от скалярного произведения вектора
от скалярного произведения вектора  на единичный вектор нормали к поверхности, т.е.
на единичный вектор нормали к поверхности, т.е.
 , где
, где 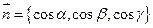 .
.
В рассматриваемой задаче
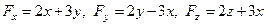 ,
,
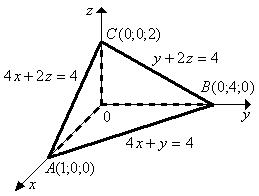
поверхность 
 является замкнутой
является замкнутой
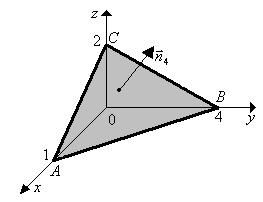
поверхностью пирамиды  , направление нормали
, направление нормали  - внешнее.
- внешнее.
Поэтому непосредственно по определению потока в данной задаче имеем:
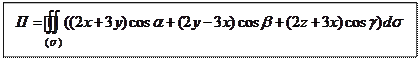
Вычисление интеграла по поверхности сводится к вычислению двойного интеграла по проекции этой поверхности на одну из координатных плоскостей.
Так как в данной задаче замкнутая поверхность  образована кусками различных плоскостей, то нужно использовать свойства аддитивности поверхностного интеграла и проводить его вычисления как сумму четырех слагаемых:
образована кусками различных плоскостей, то нужно использовать свойства аддитивности поверхностного интеграла и проводить его вычисления как сумму четырех слагаемых:
 ,
,
где 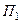 - это поток через нижнее основание
- это поток через нижнее основание 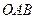 ,
,
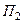 -это поток через боковую грань
-это поток через боковую грань 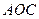 ,
,
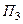 -это поток через боковую грань
-это поток через боковую грань  ,
,
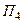 -это поток через боковую грань
-это поток через боковую грань 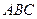 .
.
Вычисляем каждое слагаемое 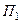 ,
, 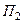 ,
, 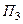 ,
, 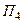 отдельно, для чего записываем проекции внешней нормали к каждой из граней пирамиды и сводим интеграл по поверхности к двойному интегралу.
отдельно, для чего записываем проекции внешней нормали к каждой из граней пирамиды и сводим интеграл по поверхности к двойному интегралу.
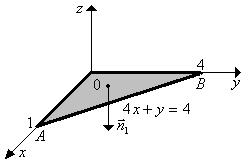
| Для 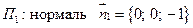 ;
уравнение поверхности (OAB): ;
уравнение поверхности (OAB): 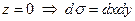 ; ;
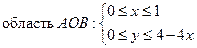
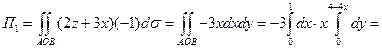

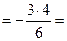 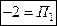 . .
|
|
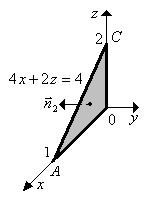
Для  ;
уравнение поверхности (OAС): ;
уравнение поверхности (OAС): 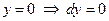 ;
область OAС: ;
область OAС: 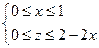
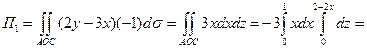
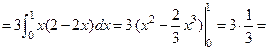 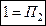 . .
|
|
|
|
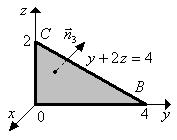
| Для  ;
уравнение поверхности (BOC): ;
уравнение поверхности (BOC): 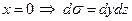 ;
область BOС: ;
область BOС: 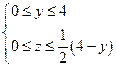

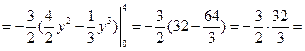  . .
|


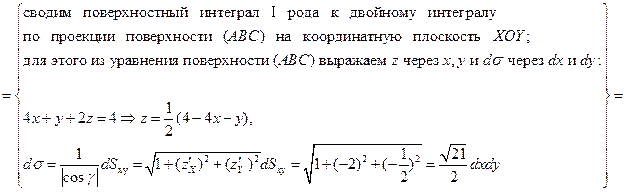
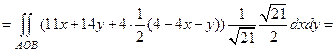
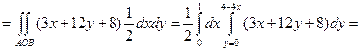
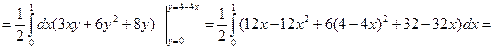
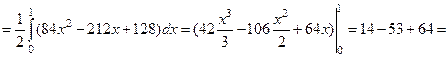
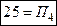 .
.
Складываем все слагаемые потока:
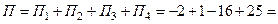
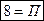 -это значение потока через замкнутую поверхность пирамиды ABCO, вычисленное непосредственно.
-это значение потока через замкнутую поверхность пирамиды ABCO, вычисленное непосредственно.
По формуле Остроградского-Гаусса:
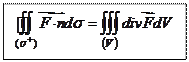 , где
, где 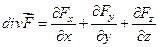 , (V) – это объем, ограниченный замкнутой поверхностью
, (V) – это объем, ограниченный замкнутой поверхностью 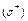 , направление нормали
, направление нормали 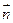 к
к
которой берется внешнее.
поэтому
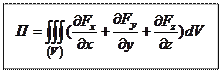
В данной задаче:
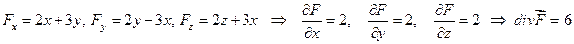
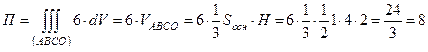 .
.
Очевидно, что значение потока, вычисленное непосредственно, и значение потока того же векторного поля, вычисленное по формуле Остроградского-Гаусса, должны совпадать.
Так как получился поток 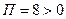 , то это означает, что в замкнутой поверхности пирамиды
, то это означает, что в замкнутой поверхности пирамиды  преобладают источники данного векторного поля над его стоками.
преобладают источники данного векторного поля над его стоками.
Ответ к задаче 8.2:  (единиц потока).
(единиц потока).

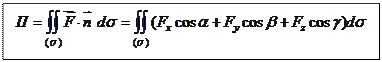 Потоком векторного поля
Потоком векторного поля  через двухстороннюю поверхность
через двухстороннюю поверхность  в направлении ее нормали
в направлении ее нормали 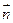 называется поверхностный интеграл по поверхности
называется поверхностный интеграл по поверхности  , где
, где 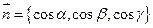 .
.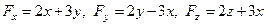 ,
,
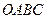 , направление нормали
, направление нормали 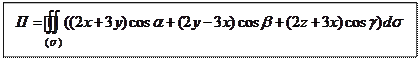
 ,
, - это поток через нижнее основание
- это поток через нижнее основание 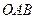 ,
,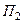 -это поток через боковую грань
-это поток через боковую грань 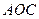 ,
,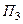 -это поток через боковую грань
-это поток через боковую грань  ,
,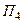 -это поток через боковую грань
-это поток через боковую грань  .
.
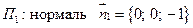 ;
уравнение поверхности (OAB):
;
уравнение поверхности (OAB): 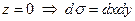 ;
;
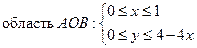
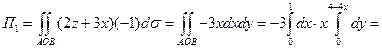

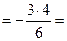
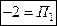 .
.

 ;
уравнение поверхности (OAС):
;
уравнение поверхности (OAС): 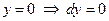 ;
область OAС:
;
область OAС: 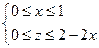
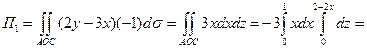
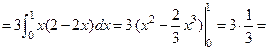
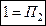 .
.

 ;
уравнение поверхности (BOC):
;
уравнение поверхности (BOC): 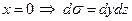 ;
область BOС:
;
область BOС: 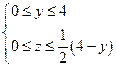

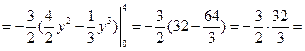
 .
.
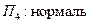
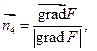
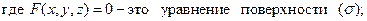
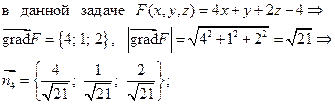


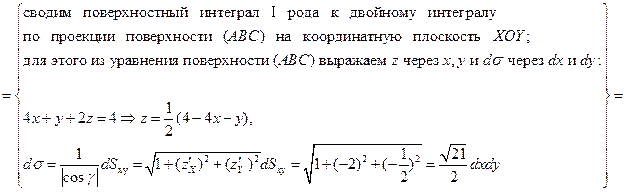
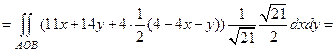
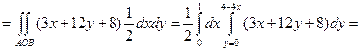
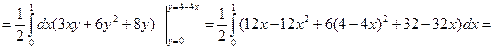
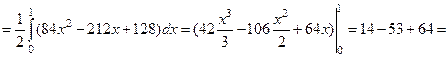
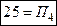 .
.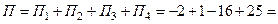
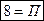 -это значение потока через замкнутую поверхность пирамиды ABCO, вычисленное непосредственно.
-это значение потока через замкнутую поверхность пирамиды ABCO, вычисленное непосредственно.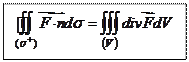 , где
, где 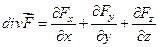 , (V) – это объем, ограниченный замкнутой поверхностью
, (V) – это объем, ограниченный замкнутой поверхностью  , направление нормали
, направление нормали 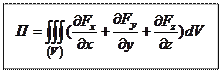
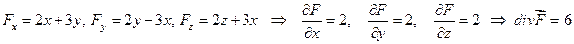
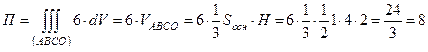 .
.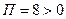 , то это означает, что в замкнутой поверхности пирамиды
, то это означает, что в замкнутой поверхности пирамиды  преобладают источники данного векторного поля над его стоками.
преобладают источники данного векторного поля над его стоками. (единиц потока).
(единиц потока).


