Собственные затухающие колебания диссипативной системы
Все реальные колебательные механические системы являются диссипативными, т.е. полная энергия такой системы постепенно расходуется на совершение работы против сил сопротивления. Поэтому реальные колебания не могут продолжаться бесконечно долго. Допустим, что на маятник кроме восстанавливающего момента силы (5) действует момент сил сопротивления (вязкого трения), пропорциональный первой производной от угла по времени, то есть угловой скорости
где r – коэффициент сопротивления. Уравнение движения (1) маятника с учетом (5) и (11) примет вид дифференциального уравнения
которое приводится к стандартному виду линейного однородного дифференциального уравнения второго порядка
Общим решением дифференциального уравнения (13) является зависимость угла поворота от времени
которая называется уравнением затухающих колебаний. График затухающих колебаний представлен на рис. 2. Движение, описываемое уравнением (14), строго говоря, является негармоническим и непериодическим, так как с течением времени последовательные максимальные отклонения точки от положения равновесия уменьшаются. Однако, при несильном затухании зависимость (14) можно рассматривать как уравнение гармонических колебаний с амплитудой затухающих колебаний, которая уменьшается с течением времени по экспоненциальному закону (пунктирная кривая на рис. 2)
где a m 0 – амплитуда колебаний в начальный момент времени t = 0; Период затухающих колебаний Т условно определяют как промежуток времени между двумя последующими максимумами колеблющейся величины a (см. рис. 2) Начальная амплитуда a m и начальная фаза колебаний φ 0 зависят от начальных условий. Частота затухающих колебаний ω зависит от собственной частоты ω0 и коэффициента затухания βи равна
то есть частота затухающих колебаний всегда меньше собственной частоты системы (ω < ω0). Для оценки быстроты затухания колебаний применяют логарифмический декремент затухания λ, определяемый как натуральный логарифм отношения амплитуд, соответствующих моментам времени, отличающимся на период Т (см. рис. 2)
Связь между логарифмическим декрементом затухания и коэффициентом затухания устанавливается формулой
Для характеристики затухания колебательной системы часто применяется величина Q, называемая добротностью, которая определяет относительную убыль энергии за период, подобно тому, как декремент затухания определяет относительную убыль амплитуды за период. Добротность обратно пропорциональна декременту затухания
С учетом формулы (17) закон убывания амплитуды (15) в зависимости от числа колебаний можно представить в виде
где n – число колебаний. Формула (20) в дальнейшем используется для экспериментального нахождения логарифмического декремента затухания λ.
|

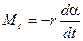 , (11)
, (11) , (12)
, (12)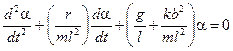 или
или  . (13)
. (13)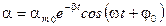 , (14)
, (14)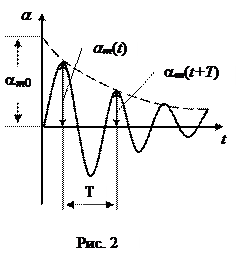
 , (15)
, (15)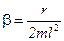 – коэффициент затухания.
– коэффициент затухания. , (16)
, (16)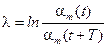 . (17)
. (17)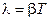 . (18)
. (18)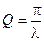 . (19)
. (19) . (20)
. (20)


