Собственные незатухающие колебания консервативной системы
Основной закон динамики для движения маятника, выведенного из положения равновесия и предоставленного самому себе, имеет вид
где J – момент инерции маятника относительно оси подвеса; e – угловое ускорение маятника; Поскольку масс стержня значительно меньше массы груза, а его длина значительно больше размеров груза, то момент инерции маятника относительно оси подвеса можно считать равным
Угловое ускорение есть вторая производная от угла по времени
Если пренебречь силами сопротивления движению, то на маятник будут действовать (см. рис. 1) два момента консервативных сил – силы тяжести
где С учетом того, что при малых углах отклонения sina» a и cosa» 1, выражение (4) можно переписать в виде
то есть при малых углах отклонения маятника от положения равновесия на нее действует восстанавливающий момент, пропорциональный углу отклонения a. Уравнение движения (1) маятника с учетом выражений (2), (3) и (5) примет вид дифференциального уравнения второго порядка
Уравнение (6) приводится к стандартному виду линейного однородного дифференциального уравнения гармонических колебаний
с циклической частотой
и периодом колебаний
Циклическая частота и период таких колебаний зависят от параметров, определяющих жесткость и инертность колеблющейся системы и не зависят от начальных условий. Они являются важнейшими характеристиками колебательной системы. Общим решением дифференциального уравнения (7) является кинематическое уравнение свободных незатухающих колебаний (или закон колебаний) в виде зависимости угла поворота от времени
где a0 – амплитуда колебаний, j0 – начальная фаза колебаний, определяемые из начальных условий и не зависящие от параметров системы. Колебания описываются функцией cos, то есть являются гармоническими.
|

 (1)
(1)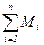 – сумма моментов сил, действующих на маятник, относительно оси подвеса.
– сумма моментов сил, действующих на маятник, относительно оси подвеса.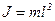 (2)
(2) . (3)
. (3)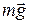 и силы упругости
и силы упругости 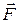 . Следовательно сумма моментов сил, действующих на маятник, относительно оси подвеса.
. Следовательно сумма моментов сил, действующих на маятник, относительно оси подвеса. (4)
(4)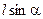 – плечо силы тяжести;
– плечо силы тяжести;  – изменение длины пружин (растяжение одной и сжатие другой пружины);
– изменение длины пружин (растяжение одной и сжатие другой пружины);  – плечо силы упругости.
– плечо силы упругости.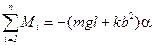 , (5)
, (5)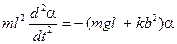 . (6)
. (6)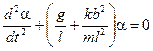 или
или  (7)
(7) (8)
(8)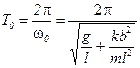 . (9)
. (9) , (10)
, (10)


