Вынужденные колебания
Вынужденные колебания маятника возникают в результате действия внешнего периодически изменяющегося момента силы. Пусть на маятник кроме восстанавливающего момента силы (5) и момента сил сопротивления (11) действует внешний вынуждающий момент силы, изменяющийся по гармоническому закону
где M0 – амплитуда вынуждающего момента, Ω – частота вынуждающего момента. Уравнение движения (1) маятника с учетом (5), (11) и (21) примет вид дифференциального уравнения
которое приводится к стандартному виду линейного неоднородного дифференциального уравнения второго порядка
Решением дифференциального уравнения (23) для установившегося режима является уравнение вынужденных колебаний.
где a m и Ω– амплитуда и частота колебаний; ψ– сдвиг фаз между вынуждающим моментом и вызываемыми им колебаниями. Из уравнения (24) следует, что при гармоническом возбуждении установившиеся вынужденные колебания представляют собой незатухающие гармонические колебания, причем частота вынужденных колебаний равначастоте Ω, вынуждающего момента. Амплитуда вынужденных колебаний определяется как свойствами силы, так и параметрами системы
Сдвиг фаз ψ определяется уравнением
из которого следует, что вынужденные колебания отстают по фазе от вынуждающего момента, и величина отставания лежит в пределах: 0 < ψ < p. Из формулы (25) следует, что при стремлении частоты Ωвынуждающего момента к собственной частоте ω0 маятника происходит резкое возрастание амплитуды колебаний. Это явление носит название резонанса. При частоте вынуждающего момента равной
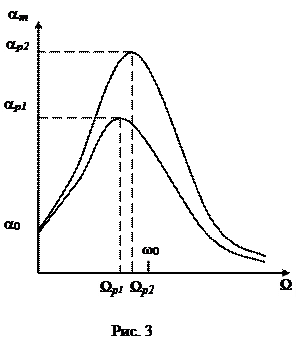
амплитуда вынужденных колебаний достигает максимального значения. Эта частота Ω Р называется резонансной частотой. Зависимость амплитуды вынужденных колебаний от частоты вынуждающего момента силы (или, что то же самое, от частоты вынужденных колебаний) называется амплитудно-частотной характеристикой системы. На рис. 3 приведены графики зависимости амплитуды вынужденных колебаний от частоты вынуждающего момента, получившие название резонансных кривых. При вынужденных колебаниях добротность (19) является важнейшей характеристикой резонансных свойств системы. Она показывает, во сколько раз амплитуда колебаний при резонансе a Р (см. рис. 3) превышает статическое смещение системы от положения равновесия a 0 при действии постоянного момента M0, когда частота Ω = 0.
При уменьшении коэффициента затухания, следовательно при увеличении добротности колебательной системы (β 2 < β 1; Q2 >Q1) резонанс проявляется более отчетливо и с большей амплитудой.
При углах отклонения маятника больше 10 – 12о заметно проявляется нелинейность, то есть не пропорциональность восстанавливающего момента силы углу отклонения a. В этом случае резонансная частота зависит от амплитуды и вид резонансной кривой искажается. Для исследуемого маятника силовая характеристика является мягкой, так как кривая зависимости М от a имеет отрицательную кривизну (см. уравнение (4)). В нелинейных системах с мягкой характеристикой восстанавливающей силы и вязким сопротивлением резонансная кривая примет вид, показанный на рис. 4. Область между вертикальными стрелками соответствует неоднозначной амплитудно-частотной зависимости. При увеличении частоты происходит «срыв колебаний» на частоте Ω2, т.е. резкое увеличение амплитуды. При уменьшении частоты наблюдается «срыв колебаний» на частоте Ω1 – резкое уменьшение амплитуды.
|
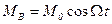, (21)
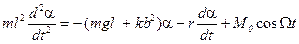, (22)
или 
. (23)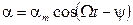
, (24)
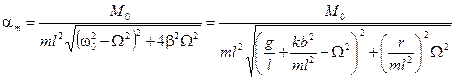. (25)
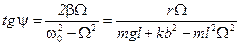, (26)
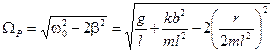. (27)
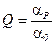. (28)
