Операции над нечеткими отношениями
Объединение двух отношений R1 и R2. mR1ÈR2 (x,y) = mR1 (x,y) Ú mR2 (x,y)
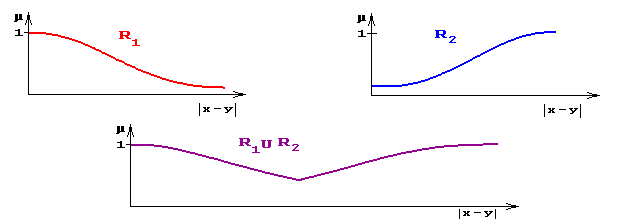
1. Ниже изображены отношения действительных чисел, содержательно означающие: x R1 y - "числа x и y очень близкие", xR2y - "числа x и y очень различны" и их объединение x R1ÈR2 y - "числа x и y очень близкие или очень различные".
где a - такое |y-x|, что mR1 (x,y) = mR2 (x,y) 2.
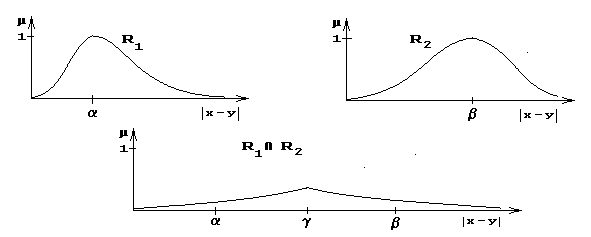
Пересечение двух отношений. Пересечение двух отношений R1 и R2 обозначается R1ÇR2 и определяется выражением: mR1ÇR2 (x,y) = mR1 (x,y) Ù mR2 (x,y) . Примеры: 1. Ниже изображены отношения: x R1 y, означающее "модуль разности |y-x| близок к a", x R2 y, означающее "модуль разности |y-x| близок к b", и их пересечение. Алгебраическое произведение двух отношений. Алгебраическое произведение двух отношений R1 и R2 обозначается R1×R2 и определяется выражением: mR1×R2 (x,y) = mR1 (x,y)× mR2 (x,y) Алгебраическая сумма двух отношений. Алгебраическая сумма двух отношений R1 и R2 обозначается R1 R1Ç(R2ÈR3) = (R1ÇR2)È(R1ÇR3), Дополнение отношения. Дополнение отношения R обозначается
. Дизъюнктивная сумма двух отношений. Дизъюнктивная сумма двух отношений R1 и R2 обозначается RÅR и определяется выражением: Обычное отношение, ближайшее к нечеткому. Пусть R - нечеткое отношение с функцией принадлежности mR (x,y). Обычное отношение, ближайшее к нечеткому, обозначается R и определяется выражением: Проекции нечеткого отношения. Пусть R - нечеткое отношение R: (x,y)®[0,1]. Первой проекцией
Аналогично, второй проекцией
Величина h(R) = Пример:
Цилиндрические продолжения проекций нечеткого отношения Проекции R1¢ и R 2¢ нечеткого отношения XRY в свою очередь определяют в X´Y нечеткие отношения
называемые, соответственно, цилиндрическим продолжением R1' и цилиндрическим продолжением R2'. Замечание. Очевидно, что для любых нечетких подмножеств А и В, определенных, соответственно, на X и Y, можно построить их цилиндрические продолжения А и В. Имеем:
и
Сепарабельность отношений Нечеткое отношение XRY называется сепарабeльным, если оно равно пересечению цилиндрических продолжений своих проекций, т.е. если R = Пример (продолжение):
т.е. исходное отношение R несепарабельно.
|

 R2 и определяется выражением:
R2 и определяется выражением: 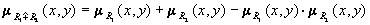 .
.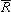 и определяется функцией принадлежности:
и определяется функцией принадлежности: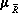 (x,y) = 1 - mR (x,y)
(x,y) = 1 - mR (x,y)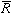 2)È(
2)È(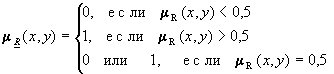
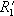 отношения R (проекция на X) называется нечеткое множество
отношения R (проекция на X) называется нечеткое множество 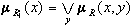 .
.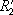 (проекцией на Y) называется нечеткое множество
(проекцией на Y) называется нечеткое множество 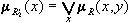 .
. называется глобальной проекцией отношения R. Если h(R)=1, то отношение R нормально, в противном случае - субнормально.
называется глобальной проекцией отношения R. Если h(R)=1, то отношение R нормально, в противном случае - субнормально.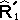 и
и 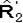 с функциями принадлежности:
с функциями принадлежности: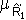 (x,y)=
(x,y)= 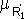 (x) при любом y,
(x) при любом y, 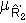 (x,y)=
(x,y)= 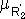 (y) при любом x,
(y) при любом x,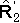 =
=



