Модель управления паровым котлом
Прототипом модели послужил паровой двигатель (лабораторный) с двумя входами (подача тепла, открытие дросселя) и двумя выходами (давление в котле, скорость двигателя). Рассмотрим одну часть задачи - управление давлением. РЕ - отклонение давления (разность между текущим и заданным значениями); Выходная лингвистическая переменная: НС - изменение количества тепла. Значения лингвистических переменных: NB - отрицательное большое; Управляющие правила (15 правил), связывающие лингвистические значения входных и выходных переменных, имеют вид: " Если отклонение давления = Аi и, если скорость отклонения давления = Вi, то изменение количества подаваемого тепла равно Сi ", где Аi, Вi, Сi - перечисленные выше лингвистические значения. Полный набор правил задавался таблицей:
Лингвистические значения отклонений задавались нечеткими подмножествами на шкалах X, Y, Z следующей таблицей:
То есть области значений входных переменных PE, CPE и выходной переменной НС представлялись 13 точками [-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6], равномерно расположенными между максимальными отрицательными и положительными значениями этих переменных.
определенной на X´Y. Ri=(Аi´Вi)´Сi, i = 1, 2,..., 15
mR i ((x,y) ,z)= (mA i (x)LmB i (y))LmC i (z). Совокупности всех правил соответствовало нечеткое отношение R = с функцией принадлежности mR(x,y,z) = При заданных значениях А¢, В¢ входных переменных регулирующее значение С¢ входной переменной определялось на основе композиционного правила вывода: С¢ = (А¢´В¢) где Функция принадлежности С¢ имеет вид: mC¢(z) = Числовое значение z 0 (изменение подаваемого тепла) определяется при этом либо из условия mC¢(z 0) = z 0 = где N - количество точек в Z (в данном случае N=13). Задача управления скоростью двигателя решалась аналогично. Результаты практического использования показали, что разработанная нечеткая модель управления сравнима с классическими моделями оптимального управления. · о полноте и непротиворечивости совокупности правил управления; · об адекватности представления правил управления вида " если А, то В " нечеткими отношениями, определяемыми разными способами; · о правильности способа вывода, основанного на (max-min)-композиции и возможности использования других видов операции композиции.
|

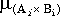 (x,y)= mA i (x)LmB i (y),
(x,y)= mA i (x)LmB i (y), Ri
Ri mR i ((x,y), z).
mR i ((x,y), z). R,
R,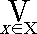
 (mA¢(x) L mB¢ (y)) L mR(x,y,z).
(mA¢(x) L mB¢ (y)) L mR(x,y,z).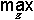 mC¢ (z),
mC¢ (z),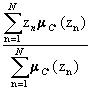 ,
,


