Правило преобразования конъюнктивной формы
Справедливо выражение:
<a есть a' и b есть b'>Þ<(a, b) есть (a'Çb')>.
Здесь Þ - знак подстановки, a'Çb' - значение лингвистической переменной (a, b), соответствующее исходному высказыванию <a есть a' и b есть b'>, которому на X´Y ставится в соответствие нечеткое множество  Ç
Ç 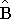 c функцией принадлежности
c функцией принадлежности
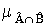 (x,y) =
(x,y) = 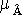 (x,y)L
(x,y)L  (x,y) = mA(x)LmB(y).
(x,y) = mA(x)LmB(y).
Правило преобразования дизъюнктивной формы
Справедливо выражение:
<a есть a' или b есть b'>Þ<(a,b) есть (a'Èb')>, где значению (a'Èb') лингвистической переменной (a, b) соответствует нечеткое множество  È
È 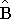 , с функцией принадлежности
, с функцией принадлежности
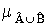 (x,y) =
(x,y) = 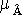 (x,y)V
(x,y)V  (x,y) = mA(x)VmB(y).
(x,y) = mA(x)VmB(y).
Замечание 1. Правила справедливы также для переменных вида <a, T1, X, G1,M1> и <a, T2, Y, G2, M2>, когда в форме значений лингвистических переменных формализованы невзаимодействующие характеристики одного и того же объекта. Например, для построения нечеткого множества высказывания < ночь теплая и очень темная > нужно использовать правило конъюнктивной формы, а для высказывания <ночь теплая или очень темная > - правило дизъюнктивной формы.
Замечание 2. Если задана совокупность лингвистических переменных {<a i, T i, X i, G i, M i >}, i = 1, 2,.., n, то любое составное высказывание, полученное из высказываний <a есть a'> с использованием модификаторов " очень ", " не ", " более или менее " и др. и связок " и ", " или ", можно привести к виду <a есть a'>, где a - составная лингвистическая переменная (a1,a2,..,a n), a' - ее значение, определяемое (как и функция принадлежности) в соответствии с вышеуказанными правилами.
Правило преобразования высказываний импликативной формы
Справедливо выражение:
<если a есть a', то b есть b'>Þ <(a, b) есть (a'®b')>, где значению (a'®b') лингвистической переменной (a, b) соответствует нечеткое отношение XRY на X´Y.
Функция принадлежности mR(x,y) зависит от выбранного способа задания нечеткой импликации.
Способы определения нечеткой импликации
Будем считать, что заданы универсальные множества X и Y, содержащие конечное число элементов. Под способом определения нечеткой импликации " если А, то В" (где А и В нечеткие множества на X и Y соответственно) будем понимать способ задания нечеткого отношения R на X´Y, соответствующего данному высказыванию.
С целью обоснованного выбора определения нечеткой импликации, японскими математиками Мидзумото, Танака и Фуками было проведено исследование всех известных по литературе определений (плюс предложенные авторами). Рассмотренные определения задавали следующие нечеткие отношения для высказывания "если А, то В":
1. Rm = (A´B)È( ´Y)
´Y)
mRm(x,y) = (mA(x)L mB(y)) V (1 - mA(x));
2. Ra = ( ´Y)Å(X´B)
´Y)Å(X´B)
mRa(x,y) = 1 L (1-mA(x) + mB(y));
3. Rc = A´B
mRc(x,y) = mA(x)L mB(y);
4. Rs = A´Y  X´B
X´B
mRs(x,y) =  ;
;
5. Rg = A´Y  X´B
X´B
mRg(x,y) = 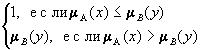 ;
;
6. Rsg = (A´Y  X´B) Ç (
X´B) Ç ( )
)
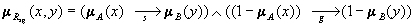 ;
;
7. Rgg = (A´Y 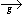 X´B) Ç (
X´B) Ç ( )
)
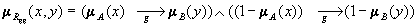 ;
;
8. Rgs = (A´Y 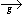 X´B) Ç (
X´B) Ç (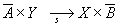 )
)
 ;
;
9. Rss = (A´Y 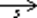 X´B) Ç (
X´B) Ç (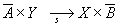 )
)
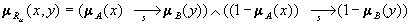 ;
;
10. Rb = ( ´Y)È(X´B)
´Y)È(X´B)
mRb(x,y) = (1-mA(x)) Ú mB(y);
11. Rà = A´Y 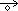 X´B
X´B
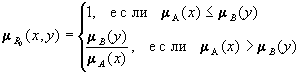 ;
;
12. R· = A´Y 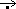 X´B
X´B
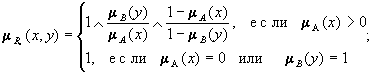
13. R* = A´Y 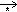 X´B
X´B
mR*(x,y) = 1 - mA(x)+ mA(x)× mB(y);
14. R# = A´Y 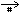 X´B
X´B
mR#(x,y)=(mA(x)Ù mB(y))Ú ((1 - mA(x)) Ù(1 - mB(y)) Ú(mB(y) Ù(1 - mA (x));
15. RÑ = A´Y 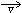 X´B
X´B

Правилом вывода являлось композиционное правило вывода с использованием (max-min)-композиции.
В качестве значений на входе системы рассматривались:
A' = A;
A' = "очень А"= А2, mA0,5(x) = mA(x)2;
A' = "более или менее А" = А0,5 mA0,5(x)= mA(x)0,5;
A' = mA(x)0,5, 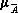 (x) = 1 - mA (x).
(x) = 1 - mA (x).
Приведем таблицу итогов исследования. В ней символ "0" означает выполнение соответствующей схемы вход-выход, символ "x" - невыполнение. Следствие "неизвестно" (Н) соответствует утверждению: "если x=A, то нельзя получить никакой информации об y".
В данной таблице первая графа -"Посылка", вторая -"Следствие".
|
|
| Rm
| Ra
| Rc
| Rs
| Rg
| Rsg
| Rgg
| Rgs
| Rss
| Rb
| Rà
| R·
| R*
| R#
| RÑ
|
| A
| B
| x
| x
|
|
|
|
|
|
|
| x
| x
| x
| x
| x
| x
|
| A2
| B2
| x
| x
| x
|
| x
|
| x
| x
|
| x
| x
| x
| x
| x
| x
|
| A2
| B
| x
| x
|
| x
|
| x
|
|
| x
| x
| x
| x
| x
| x
| x
|
| A0,5
| B0,5
| x
| x
| x
|
|
|
|
|
|
| x
| x
| x
| x
| x
| x
|
| A0,5
| B
| x
| x
|
| x
| x
| x
| x
| x
| x
| x
| x
| x
| x
| x
| x
|

| Н
|
|
| x
|
|
| x
| x
| x
| x
|
|
|
|
| x
| x
|
| A
| B
| x
| x
| x
| x
| x
|
|
|
|
| x
| x
| x
| x
| x
| x
|
Кроме ответа о выполнении соответствующей схемы (0 или х),авторами исследованы явные выражения для функций принадлежности следствий по каждому из вариантов определения нечеткой импликации, на основе чего ими был сформулирован вывод:
- Rm и Ra не могут быть использованы;
- Rc может использоваться частично; - Rs, Rg, Rsg, Rgg, Rgs, Rss рекомендованы к использованию;
- Rb, Rà, R·, R*, R#, RÑ не рекомендованы к использованию.

 Ç
Ç 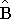 c функцией принадлежности
c функцией принадлежности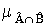 (x,y) =
(x,y) = 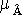 (x,y)L
(x,y)L  (x,y) = mA(x)LmB(y).
(x,y) = mA(x)LmB(y).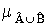 (x,y) =
(x,y) =  ´Y)
´Y) X´B
X´B ;
; X´B
X´B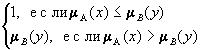 ;
; )
)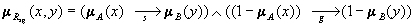 ;
;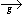 X´B) Ç (
X´B) Ç (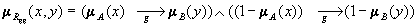 ;
;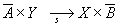 )
)  ;
;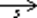 X´B) Ç (
X´B) Ç (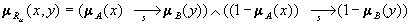 ;
;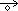 X´B
X´B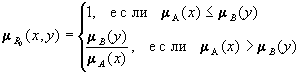 ;
;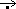 X´B
X´B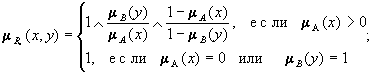
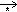 X´B
X´B 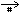 X´B
X´B 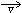 X´B
X´B 
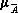 (x) = 1 - mA (x).
(x) = 1 - mA (x). 



