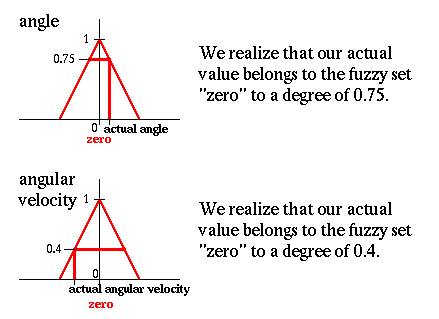Этапы процесса нечеткого вывода
Процесс нечеткого вывода распадается на 5 этапов. 1. Определение и интерпретация входных переменных и их пределов. 2. Определение и интерпретация выходных переменных и их пределов. 3. Определение функции принадлежности для каждой входной и выходной переменной. 4. Составление базы правил, которая будет отвечать за управляющие операции. 5. Переход от нечеткости к конкретным числовым значениям. Этап 1 Определение и интерпретация входных переменных и их пределов Имеются 2 входные переменные. • Оценка техники игры. • Рост игроков. Характеристики оценки игры. (0-100 баллов).
Характеристики роста игроков (см).
Этап 2 Определение и интерпретация выходных переменных и их пределов Имеется 1 выходная переменная. • Уверенность отбора в команду (К) Характеристика уверенности отбора в команду (О-100%)
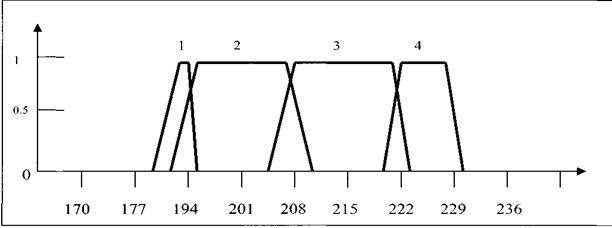
Определение функции принадлежности для каждой входной и выходной переменной Нижнее и верхнее значения определяют трапецеидальную функцию принадлежности для каждой входной и выходной переменной. 1. Функции принадлежности для оценки техники игры
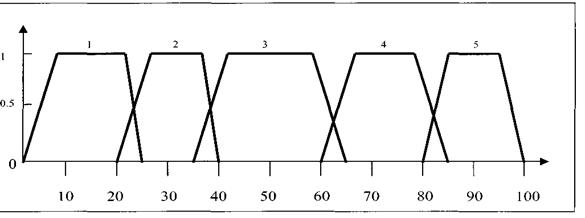
2. Функции принадлежности для оценки роста
3. Функции принадлежности для уверенности отбора
Составление базы правил
База правил представлена в таблице
Каждая ячейка базы правил определяется как сложение (логическое И) входов, чтобы определить отдельный вход. Каждая ячейка базы правил определяется как сложение (логическое И) входов, чтобы определить отдельный выход. Например затемненная ячейка означает: Если (техника игры) = (хорошо) И (рост) = (очень высокий) Тогда (уверенность отбора) = (полная). Этап 5 Переход от нечеткости к конкретным числовым значениям Предположим: Техника игры оценивается 47 баллов. Рост 206 см. Теперь необходимо определить, какая функция принадлежности активизирована и в какой степени. Из графиков функций принадлежностей видно, что в данном случае активизированы 4 функции принадлежности: • «Очень хорошая техника игры» • «Не очень хорошая техника игры» • «Высокий рост» • «Не очень высокий рост» В базе правил активизированы 4 правила.
Скомбинируем значения функции принадлежности, используя логическое "И". Правило 1. (F-хорошая) И (F-высокая) = min(0.4, 0.9) = 0.4 Правило 2. (F-хорошая) И (F-не очень высокая) = min(0.4,0.6) = 0.4 Правило 3. (F-не очень хорошая) И (F-высокая) = min(0.6,0.9) = 0.6 Правило 4. (F-не очень хорошая) И (F-не очень высокая) = min(0.6,06) = 0.6 Полученные величины определяют область пересечения для выходных значений. Области пересечения показаны ниже, на диаграмме функций принадлежностей для уверенности отбора. Функции принадлежности для уверенности отбора
Теперь необходимо определить центр но формуле: I Xi |J,A[Xi] 0.4*82+0.4*63+0.6*65+0.6*25 Центр= —————— = ———-—————————.— = 56% S JlA[Xi] 0.4+0.4+0.6+0.6 Таким образом, 56% - значение коэффициента уверенности для отбора претендента в баскетбольную команду, для входных данных: рост - 206 см и техника игры - 47 баллов.
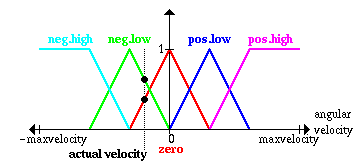
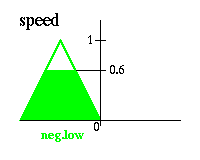
Контроллеры нечеткой логики - наиболее важное приложение теории нечетких множеств. Их функционирование немного отличается от работы обычных контроллеров; для описания системы используются знания экспертов вместо дифференциальных уравнений. Эти знания могут быть выражены естесственным образом с помощью лингвистических переменных, которые описываются нечеткими множествами. Пример: Перевернутый маятник Проблема состоит в балансировке вертикальной мачты, подвижно закрепленной нижним концом на тележке, которая может двигаться только в двух направлениях - влево или вправо. · отрицательная высокая, neg.high (голубой) · отрицательная низкая, neg.low (зеленый) · нулевая, zero (красный) · положительная низкая, pos.low (синий) · положительная высокая, pos.high (розовый)
Тоже самое делается для угла между тележкой и мачтой маятника и для угловой скорости изменения этого угла
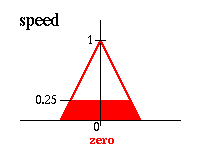
Пожалуйста заметьте, что для упрощения предполагается, что начальное положение мачты около центра справа, так что угол более чем, скажем, 45 градусов в любом направлении по определению никогда не возникнет. На следующей странице определим некоторые правила, которые желательно применить в данной ситуации. Сейчас определим несколько правил, которые определяют что делать в данной ситуации. Положим, например, что мачта находится справа (угол равен нулю) и не двигается (угловая скорость - ноль). Очевидно, что это желаемое положение, и ничего предпринимать не надо (скорость равна нулю). Итак, получаем два правила, которые более формально представляются в следующей форме: · Если угол равен нулю И угловая скорость равна нулю, тогда скорость должна быть равна нулю. · Если угол равен нулю И угловая скорость положительная низкая, тогда скорость должна быть положительной низкой.
Сведем все полученные правила в таблицу:
| угол | скорость | ОВ ОН 0 ПН ПВ -----------+------------------------------ ОВ | ОВ угл. ОН | ОН 0 скор. 0 | ОВ ОН 0 ПН ПВ ПН | 0 ПН ПВ | НВ
где ОВ - Отрицательное Высокое (большое) значение, ОН - Отрицательное Низкое (малое) значение, 0 - нуль и т.д. Для дальнейших расчетов определим численные значения для угла и угловой скорости. Рассмотрим следующую ситуацию: Реальное значение угла:
Реальное значение угловой скорости:
Применим правило Если угол равен нулю И угловая скорость равна нулю, тогда скорость равна нулю к реальным значениям переменных.
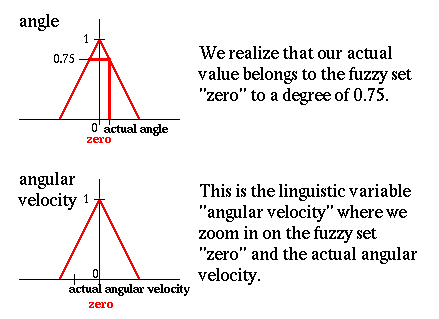
Проследим получение результата с помощью нечеткого вывода. 1. Если угол равен нулю И угловая скорость равна нулю тогда скорость равна нулю
Получаем, что реальное значение угла принадлежит нечеткому множеству "ноль" со степенью 0.75. 2. Если угол равен нулю И угловая скорость равна нулю тогда скорость равна нулю
Реальное значение угла принадлежит нечеткому множеству "ноль" со степенью 0.75. 3. Если угол равен нулю И угловая скорость равна нулю тогда скорость равна нулю
Реальное значение угла принадлежит нечеткому множеству "ноль" со степенью 0.75. Реальное значение угловой скорости принадлежит нечеткому множеству "ноль" со степенью 0.4. 4. Если угол равен нулю И угловая скорость равна нулю тогда скорость равна нулю
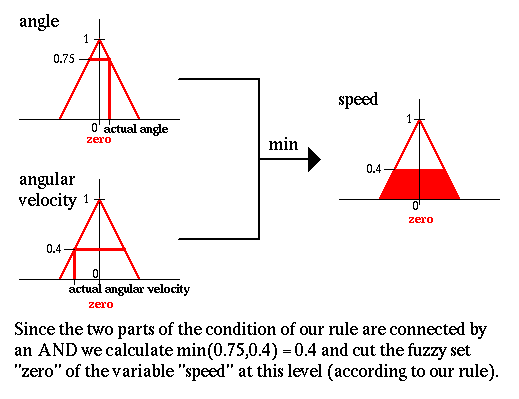
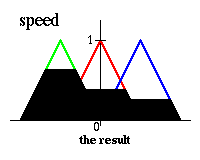
Только четыре правила приводят к результату. Объединим их в одно решение. Таким образом результатом правила Если угол равен нулю И угловая скорость равна нулю тогда скорость равна нулю является:
Результатом правила Если угол равен нулю И угловая скорость отрицательная низкая тогда скорость - отрицательная низкая является: Результатом правила Если угол положительный малый И угловая скорость равна нулю тогда скорость - положительная низкая
Результатом правила Если угол положительный малый И угловая скорость отрицательная низкая тогда скорость равна нулю является: Объединение этих четырех результатов дает общее решение: Таким образом, решением контроллера нечеткой логики является нечеткое множество (для скорости). Далее необходимо выбрать одно значение для представления конечного выходного значения. Существует несколько эвристических методов (методов дефаззификации), один из которых, например, предполагает выбирать в качестве конечного значения центр тяжести нечеткого множества:
Вся данная процедура получения решения называется контроллером Мамдани (Mamdani controller).
|

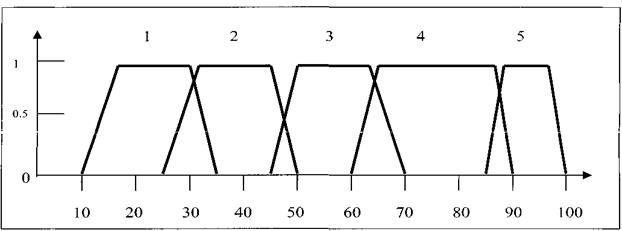

 Нечеткое управление
Нечеткое управление