Нечеткие множества

 

Нечеткая логика возникла как наиболее удобный способ построения систем управления метрополитенами и сложными технологическими процессами, а также нашла применение в бытовой электронике, диагностических и других экспертных системах. Несмотря на то, что математический аппарат нечеткой логики впервые был разработан в США, активное развитие данного метода началось в Японии, и новая волна вновь достигла США и Европы.
В Японии до сих пор продолжается бум нечеткой логики и экспоненциально увеличивается количество патентов, большая часть которых относится к простым приложениям нечеткого управления.

Термин fuzzy (англ. нечеткий, размытый) В Японии исследования в области нечеткой логики получили широкую финансовую поддержку. В Европе и США усилия были направлены на то, чтобы сократить огромный отрыв от японцев. Так например, агенство космических исследований NASA стало использовать нечеткую логику в маневрах стыковки.

Нечеткая логика является многозначной логикой, что позволяет определить промежуточные значения для таких общепринятых оценок, как да|нет, истинно|ложно, черное|белое и т.п. Выражения подобные таким, как слегка тепло или довольно холодно возможно формулировать математически и обрабатывать на компьютерах.
Нечеткая логика появилась в 1965 в работах Лотфи А. Задэ (Lotfi A. Zadeh),профессора технических наук Калифорнийского университета в Беркли.

Что такое нечеткое множество?

Самым главным понятием систем, основанных на нечеткой логике, является понятие нечеткого (под)множества.

Из классической математики известно понятие четких (определенных) множеств.

 

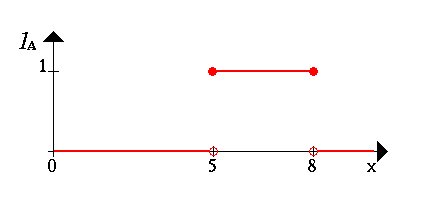
Пример:

Рассмотрим множество X всех чисел от 0 до 10, котрое назовем универсумом рассуждения. Определим подмножество A множества X всех действительных чисел от 5 до 8.

A = [5,8]

Покажем характеристическую функцию множества A, эта функция ставит в соответсвие число 1 или 0 каждому элементу в X, в зависимости от того принадлежит данный элемент подмножеству A или нет. Результат представлен на следующем рисунке:

 

Можно интерпретировать элементы, которым поставлена в соответствие 1, как элементы, находящиеся во множестве A, а элементы, которым поставлен в соответствие 0, как элементы, не находящиеся во множестве A.

Эта концепция используется во многих областях приложений. Но можно легко обнаружить ситуации, в которых данной концепции будет недоставать гибкости.

В данном примере опишем множество молодых людей. Более формально можно записать так

B = {множество молодых людей}

Так как, вообще, возраст начинается с 0, то нижний предел этого множества должен быть нолем. Верхний предел определить немного сложнее. На первый раз установим верхний предел, скажем, равным 20 годам. Таким образом, получаем B как четко ограниченный интервал, буквально:

B = [0,20]

Возникает вопрос: почему кто-то в свой двадцатилетний юбиоей - молодой, а сразу на следующий день уже не молодой? Очевидно, это структурная проблема, и если передвинуть верхнюю границу в произвольную точку, то можно задаться точно таким же вопросом.

Более естественный путь получения множества B состоит в ослаблении строгого разделения на молодых и не молодых. Сделаем это, вынося не только (четкие) суждения Да, он|она принадлежит множеству молодых людей или Нет, он|она не принадлежит множеству молодых люей, но и более гибки формулировки ДА, он|она принадлежит к достаточно молодым людям или Нет, он|она не очень молод|молода.

На следующей странице рассмотрим как с помощью нечеткого множества определить такое выражение, как он|она еще молоды.

мы используем нечеткие множества, чтобы сделать компьютер более умным. Представим эту мысль более формализованно. В первом примере мы кодировали все элементы универсума рассуждения с помощью 0 или 1. Простой способ обобщить данную концепцию - ввести значения между 0 и 1. Реально можно даже допустить бесконечное число значений между 0 и 1, называемое единичным интервалом I = [0, 1].

Интерпретация чисел при соотнесении всех элементов универсума рассуждений становится теперь более сложной. Конечно, снова число 1 ставится в соответствие (соотносится) тому элементу, который принедлежит множеству B, а 0 означает, что элемент точно не принадлежит множеству B. Все другие значения определяют степень принадлежности ко множеству B.

Для наглядности приведем характеристическую функцию множества молодых людей, как и в первом примере.

То есть 25-летние все еще молоды со степенью 50 процентов.

Теперь вы поняли что такое нечеткое множество. Но что с ним можно делать?

Операции с нечеткими множествами

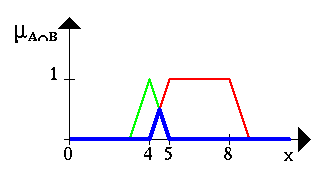
Сейчас, когда мы уже знаем, что такое нечеткие множества, попытаемся определить базовые операции (действия) над нечеткими множествами. Аналогично действиям с обычными множествами нам потребуется определить пересечение, объединение и отрицание нечетких множеств. В своей самой первой работе по нечетким множествам Л. А. Задэ предложил оператор минимума для пересечения и оператор максимума для объединения двух нечетких множеств. Легко видеть, что эти операторы совпадают с обычными (четкими) объединением и пересечением, только рассматриваются степени принадлежности 0 и 1.

Чтобы пояснить это, приведем несколько примеров. Пусть A нечеткий интервал от 5 до 8 и B нечеткое число около 4, как показано на рисунке.

Следующий пример иллюстрирует нечеткое множество между 5 и 8 И (AND) около 4 (синяя линия).

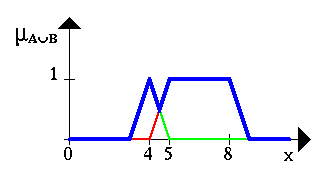
Нечеткое множество между 5 и 8 ИЛИ (OR) около 4 показано на следующем рисунке (снова синяя линия).

Следующий рисунок иллюстрирует операцию отрицания. Синяя линия - это ОТРИЦАНИЕ нечеткого множества A.