Субъективный Байесовский метод
Введем определения.
Условная вероятность события d при данном s – это вероятность того, что событие d наступит при условии, что наступило событие s. Напрмер, вероятность того, что пациент действительно страдает заболеванием d, если у него обнаружен только симптом s. В традиционной теории вероятностей для вычисления условной вероятности события d при данном s используется следующая формула:
Из формулы видно, что вероятность определяется в терминах совместимости событий. Она представляет собой отношение вероятности совпадения событий d и s к вероятности появления события s. Из предыдущей формулы следует, что
Если разделить обе части на P(s) и подставить в правую часть (1), то получим правило Байеса в простейшем виде:
Это правило, которое еще называют инверсной формулой для условной вероятности, позволяет определить вероятность P(d|s) появления события d, при условии, что произошло событие s через известную условную вероятность P(s|d). В полученном выражении P(d) – априорная вероятность наступления события d, а P(d|s)- апостериорная вероятность, то есть вероятность того, что событие s свершилось.
В системах, основанных на знаниях, чаще всего используется формула (3). Например, существует некий пациент с симптомом заболевания – “боль в груди” и желательно знать какова вероятность того, что этот симптом является следствием определенного заболевания (например, инфаркта миокарда). Для того чтобы вычислить вероятность
P(инфаркт миокарда | боль в груди)
по формуле (1) необходимо знать (или оценить каким-либо способом) сколько человек в мире страдают этим заболеванием и сколько из них жалуются на боль в груди. Как правило получить такого рода информацию сложно, поэтому формула (3) больше пригодна для практического применения.
Например, врач на основании собственного опыта может оценить, у какой части пациентов, страдающих этим заболеванием, встречается данный симптом. Следовательно, он может оценить значение вероятности P(боль в груди | инфаркт миокарда).
Субъективный взгляд на природу вероятности тесно связан с правилом Байеса по следующей причине. Предположим, мы располагаем достаточно достоверной оценкой вероятности P(s| d), где s- означает симптом, а d- заболевание. Тогда по формуле (3) можно вычислить вероятность P(d|s). Оценку вероятности P(d) можно взять из публикуемой медицинской статистики, а оценить значение P(s) врач может на основании собственных наблюдений. Надо отметить, что вычисление P(d|s) не вызывает затруднений, когда речь идет о единственном симптоме, учитывающемся при диагностике одного заболевания. Если же задача ставится как диагностика m различных заболеваний по n – различным симптомам, то задача усложняется вычислением (mn)k+m+nk оценок вероятностей.
|

 (1)
(1)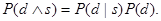 (2)
(2) (3)
(3)


