Решение некоторых задач теплопроводности
1. Нестационарная задача теплопроводности для неограниченной пластины с граничными условиями 3 рода. Рассмотрим неограниченную пластину толщиной 2h. Если толщина пластины мала по сравнению с длиной и шириной, то такую пластину считают неограниченной. Изменение температуры происходит только в одном направлении x, в двух других направлениях температура не изменяется (¶T/¶ y = ¶T/¶ z = 0), следовательно, задача является одномерной. Начальное распределение температуры задано некоторой функцией T(x, 0) = f (x). Охлаждение (нагревание) происходит в среде с постоянной температурой Tс = const. На обеих поверхностях отвод теплоты осуществляется при постоянном во времени коэффициенте теплоотдачи. При заданных граничных условиях коэффициент теплоотдачи одинаков для всех точек поверхности пластины. Отсчет температуры пластины для любого момента времени будем вести от температуры окружающей среды, т. е. T – Tс = q. Так как задача в пространстве одномерная, то дифференциальное уравнение теплопроводности имеет вид:
Начальные условия:
При заданных условиях охлаждения (нагревания) задача является симметричной, поэтому начало координат поместим на оси пластины. При этом граничные условия на оси и на поверхности пластины запишутся в виде:
Дифференциальное уравнение (1.1) совместно с начальным (1.2) и граничными (1.3) условиями формулируют поставленную задачу. Решение. Решение дифференциального уравнения (1.1) ищем в виде произведения двух функций, из которых одна является функцией только t, а другая – только x (метод разделения переменных):
После подстановки последнего выражения в дифференциальное уравнение (1.1) получим:
или
В этом уравнении переменные легко разделяются, и его можно записать следующим образом:
Левая часть уравнения (1.5) есть функция только t, а правая – функция только x. Так как равенство (1.5) должно иметь место при любых значениях x и t, то обе его части должны быть равны одной и той же постоянной величине. откуда
Постоянную k определим из граничных условий, а знак минус выбираем из физических соображений, так как тепловые процессы стремятся к тепловому равновесию. В результате получим систему обыкновенных дифференциальных уравнений (1.6) и (1.7), которые легко интегрируются. Уравнению (1.6) удовлетворяет функция Уравнению (1.7) удовлетворяет функция
Подставляя полученные выражения для j(t) и y(x) в уравнение (1.4), получаем частное решение:
Выражение (1.8) удовлетворяет исходному уравнению (1.1) при любых значениях постоянных C 1, C 2, C 3 и k. Чтобы уравнение (1.8) было решением поставленной задачи, оно должно удовлетворять начальным и граничным условиям. Используя граничное условие при x =0
находим:
или
откуда C 2 = 0. Это значит, что частное решение y(x) = C 2 sin(kx) должно быть исключено как не удовлетворяющее заданным граничным условиям. Если учесть, что C 2 = 0, и обозначить C 1 C3 = A, то уравнение (1.8) можно записать в виде
Применив граничное условие
получим:
После преобразования (1.10) получим:
где a h /l = Bi (критерий Био). Если обозначить kh = m, то последнее выражение можно записать следующим образом:
Решение характеристического уравнения (1.11) дает бесконечное множество значений корней этого уравнения, т.е. величин m n, причем каждое последующее больше предыдущего:
Важно отметить, что каждому значению числа Bi отвечает своя совокупность корней уравнения (1.11). При Bi → ∞ характеристическое уравнение имеет вид: cos μ = 0, и корни уравнения будут равны:
Значение Bi → ∞ соответствует интенсивному теплообмену поверхности со средой. При этом граничное условие 3 рода переходит в граничное условие 1 рода, т.е. заданию постоянной температуры на поверхности пластины. При Bi → 0 корни уравнения (1.11) равны:
где n = 1, 2, 3... Для других конечных значений числа Bi величины m n имеют промежуточные значения. Следовательно, каждому найденному значению корня m будет соответствовать свое частное распределение температуры:
Общее решение можно представить суммой частных решений, т.е. бесконечным рядом:
Известно, что если отдельные распределения (1.12) удовлетворяют дифференциальному уравнению (1.1) и граничным условиям (1.3), то и сумма их также удовлетворяет тем же условиям. Постоянную An в уравнении (1.13) находим из начального условия: Уравнение (1.14) есть разложение четной функции в ряд Фурье с заданными параметрами m n, определяемыми характеристическим уравнением (1.11). Для этой последовательности чисел m n справедлива формула
с помощью которой можно определить все значения коэффициентов An в уравнении (1.14). Для этого умножим обе части уравнения (1.14) на cos(mn x /h) и затем проинтегрируем полученное соотношение по толщине пластины, тогда
так как все остальные слагаемые в правой части, для которых n ¹ m, обращаются в нуль. Интеграл в правой части соотношения (1.15) равен
Из уравнения (1.16) следует, что An является функцией только корня характеристического уравнения и начального распределения температуры. Подставив полученное выражение для постоянной An в уравнение (1.13), получим уравнение для температурного поля при охлаждении (нагревании) однородной пластины
Уравнение (1.17) позволяет получить значение температуры в любой точке пластины для любого момента времени t при любом начальном распределении температуры q0. Если в начальный момент времени (t = 0) температура в пластине распределена равномерно, т. е. T0 – Tс = q0 = const, то интеграл в уравнении (1.16) равен (q0×2h/m n) sin m n. При этом выражение для An принимает вид:
Подставляя значение An в уравнение (1.17), получаем:
Или в безразмерной форме:
Где q/q0 = Q – безразмерная температура; x /d = X – безразмерная координата; a t/h2 = Fo – число Фурье, представляющее собой безразмерное время.
|

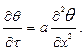 (1.1)
(1.1) (1.2)
(1.2)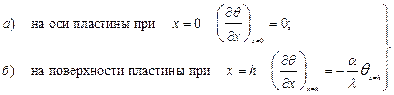 (1.3)
(1.3)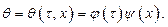 (1.4)
(1.4)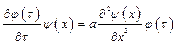

 (1.5)
(1.5)
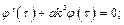 (1.6)
(1.6)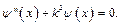 (1.7)
(1.7) .
.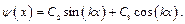
 (1.8)
(1.8)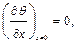
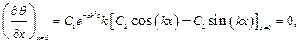
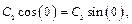
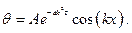 (1.9)
(1.9)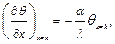
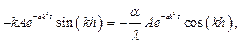 (1.10)
(1.10)
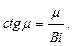 (1.11)
(1.11)
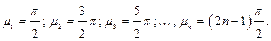
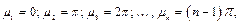
 (1.12)
(1.12) (1.13)
(1.13) (1.14)
(1.14)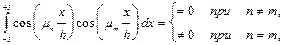
 (1.15)
(1.15)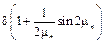 , тогда
, тогда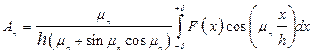 (1.16)
(1.16)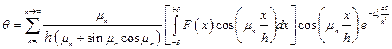 (1.17)
(1.17)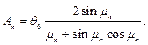 (1.18)
(1.18)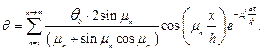 (1.19)
(1.19)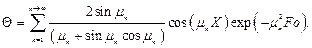 (1.20)
(1.20)



