ОПРЕДЕЛЕНИЕ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК В СРЕДЕ ПОСТОЯННОЙ ТЕМПЕРАТУРЫ ПРИ НАЛИЧИИ ИСТОЧНИКА ТЕПЛА
Рассмотрим методы определения теплофизических характеристик, реализация которых предполагает задание граничного условия второго рода и граничного условия первого рода, т. е. наличие источников и стоков тепла. Под источником понимается пространственно-локализованный тепловой источник постоянной электрической мощности. Одновременное действие тепловых источников и стоков приводит тело в стационарное состояние, в режиме которого обычно определяется коэффициент теплопроводности. Во всех случаях стационарному состоянию предшествует нестационарный режим, который используется для определения коэффициента температуропроводности. Создается, таким образом, возможность осуществить комплексное определение теплофизических характеристик в течение одного непрерывно протекающего эксперимента. НЕСТАЦИОНАРНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК В НАЧАЛЬНОЙ СТАДИИ ТЕПЛООБМЕНА Рассмотрим экспериментальные методы, в которых исследуемый образец считается телом неограниченной протяженности в направлении распространения температурного поля за время проведения эксперимента. Преимущество таких методов состоит в исключении граничных условий третьего или первого рода, которые трудно реализовать с высокой степенью точности. Метод источника постоянной мощности относится к чисто нестационарным методам, основанным на закономерностях начальной стадии развития температурного поля в полуограниченном теле, нагреваемом источником постоянной мощности. Основным достоинством метода является кратковременность проведения эксперимента. К недостаткам данного метода, как и вообще всех чисто нестационарных методов, следует отнести зависимость конечных результатов от начального теплового состояния исследуемого образца. Рассмотрим полуограниченное тело, начальная температура которого Т0. Ограничивающая поверхность нагревается постоянным тепловым потоком q=const. Изменение температуры происходит в одном направлении.
Решение такой задачи имеет вид:
Если температуру измерять в плоскости нагревателя (х=0), то из (6.1) следует
т.к. Отношение
характеризует аккумуляционную тепловую способность тела и носит название коэффициента тепловой активности тела. При введении коэффициента тепловой активности в (6.2) получим
Графическое изображение уравнения (6.3) в координатах
Из (6.4) получаем формулу для расчета коэффициента тепловой активности
Удельный тепловой поток q рассчитывается по формуле
где I, U, RH, S - соответственно величины тока, напряжения, сопротивления и площадь одной стороны нагревателя. Коэффициент температуропроводности определяется по времени запаздывания, т.е. времени, в течение которого температура в сечении x станет такой же, как температура образца в плоскости нагревателя в момент времени τ1. Для разных моментов времени τ1 и τ2 (τ2 > τ1) можно написать:
или
следовательно,
Производя преобразования, получим:
Введем обозначения:
Тогда из (6.8) получаем:
Значение величины N определяют по формуле (6.9), в которую входят экспериментально измеряемые величины. Используя таблицу
Коэффициент теплопроводности и удельную теплоемкость находят из соотношений
Одновременно расчет коэффициента температуропроводности можно провести по найденным из эксперимента отношениям избыточных температур
Обозначим
Тогда
Таким образом, в данном случае расчет коэффициента температуропроводности сводится к нахождению аргумента Х1 по таблице при найденных из эксперимента значениях N1, соответствующих определенным моментам времени τ. В любом случае комплексное определение теплофизических характеристик на основе решения (6.1) предполагает знание характера изменения температуры во времени в каких-либо двух точках исследуемого образца. На рис. 4 представлена схема измерительной ячейки.
Рис. 4. Схема измерительной ячейки. Графическое изображение зависимости D T н = f (
На рис. 5 показаны возможные отклонения D T н от теоретической зависимости 1. Кривая 2 показывает, что теплоемкость используемого нагревателя велика; кривая 3 свидетельствует о значительной величине термического сопротивления в месте контакта нагревателя с двумя полубесконечными стержнями. Кривая 4 показывает, что в опыте начинают сказываться боковые утечки тепла и проводить его дальше нецелесообразно.
|

 (6.1)
(6.1)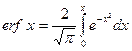


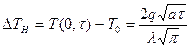 (6.2)
(6.2)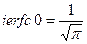
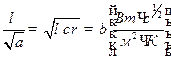
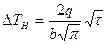 (6.3)
(6.3)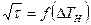 представляет собой прямую линию, проходящую через начало координат с тангенсом угла наклона к оси абсцисс, равным
представляет собой прямую линию, проходящую через начало координат с тангенсом угла наклона к оси абсцисс, равным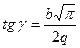 (6.4)
(6.4)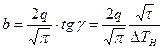 (6.5)
(6.5)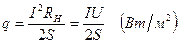 , (6.6)
, (6.6)

 (6.7)
(6.7) (6.8)
(6.8)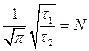 (6.9)
(6.9)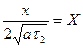 (6.10)
(6.10)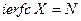 (6.11)
(6.11)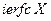 , находят соответствующее значение аргумента X, значение которого позволяет из (6.10) получить формулу для расчета коэффициента температуропроводности:
, находят соответствующее значение аргумента X, значение которого позволяет из (6.10) получить формулу для расчета коэффициента температуропроводности:
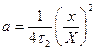 (6.12)
(6.12)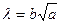 (6.13)
(6.13) (6.14)
(6.14)
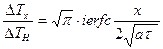 (6.15)
(6.15)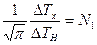 (6.16)
(6.16) (6.17)
(6.17)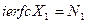 (6.18)
(6.18)
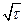 ) представляет собой прямую линию, проходящую через начало координат, с тангенсом угла наклона, определяемым значением коэффициента тепловой активности. Прямолинейность этой зависимости с момента включения нагревателя указывает на правильность хода эксперимента и на выполнение всех требуемых теоретически постулированных граничных условий, что является основным преимуществом рассмотренной методики расчета теплофизических характеристик.
) представляет собой прямую линию, проходящую через начало координат, с тангенсом угла наклона, определяемым значением коэффициента тепловой активности. Прямолинейность этой зависимости с момента включения нагревателя указывает на правильность хода эксперимента и на выполнение всех требуемых теоретически постулированных граничных условий, что является основным преимуществом рассмотренной методики расчета теплофизических характеристик.



