ИМПУЛЬСНЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК
Закономерности развития нестационарных температурных полей, создаваемых действием мгновенных точечных, линейных или плоских источников тепла в неограниченном теле, явились основой для создания импульсных методов комплексного определения теплофизических характеристик различных материалов. Общее решение дифференциального уравнения теплопроводности для случая действия мгновенного точечного источника тепла в точке (x 1, y 1, z 1) неограниченного тела имеет вид:
где Q — количество тепла, выделяемое в точке (x 1, y 1, z 1) неограниченного тела в момент времени t = t (t > t). Выражение для двумерного температурного поля Q1(x, y, t), создаваемого линейным мгновенным источником тепла Q 1, Дж / м, действующим в момент времени t = t на прямой, параллельной оси z и проходящей через точку (x 1, y 1), получается интегрированием выражения (7.1) по dz 1в пределах от –¥ до +¥, т. е.
Здесь Если проинтегрировать выражение (7.2) по dy 1в пределах от –¥ до +¥, то получается решение одномерного уравнения теплопроводности для функции Q2(x, t) в случае действия мгновенного плоского источника тепла Q s, Дж / м 2, в плоскости x = x 1:
Здесь МЕТОД ИМПУЛЬСНОГО ЛИНЕЙНОГО ИСТОЧНИКА ТЕПЛА Следует учесть, что мгновенный тепловой источник — математическая абстракция. На практике «мгновенность» реализуется путём задания кратковременного теплового импульса. Такой импульс может быть создан, например, за счёт действия электрического или лазерного источника. Необходимо, таким образом, рассматривать задачу о действии источника в течение некоторого времени
где
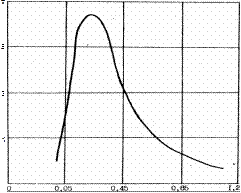
Интегрирование (7.4) по времени не налагает каких-либо ограничений на величину времени, т.е. на продолжительность теплового воздействия. Если источник действует достаточно долго, то мы не получим кривую с выраженным максимумом (рис. 6). Температура в некоторой точке будет монотонно расти. Чтобы получить экспериментально кривую, подобную рис. 6, необходимо задать короткий тепловой импульс. Идея метода и состоит в исследовании экспериментальной зависимости Значение максимума избыточной температуры
Если продифференцировать выражение (7.5) по
(в дальнейшем будем писать вместо Далее всё сводится к преобразованию (7.6)
Введём
Тогда соотношение (7.7) можно переписать в виде
Интегрируя первый интеграл (7.8) по частям, получим:
Следовательно,
Последнее соотношение можно переписать в виде
Логарифмируя, найдём
Откуда
Введём обозначение:
Тогда (7.9) запишется в виде
Выражение (7.11) связывает температуропроводность с экспериментально определяемыми величинами. Формула для расчёта коэффициента теплопроводности получается путём преобразования (7.5):
Дальнейшие выкладки аналогичны приведенным выше. Введём переменную
Тогда
Так как
где Таким образом, коэффициент теплопроводности определяется по формуле (7.12). Коэффициент температуропроводности
где Теплоёмкость вычисляется по формуле
где Значения Удельный тепловой поток, входящий в расчётные соотношения, вычисляется по формуле:
На рис. 7 показана схема исследования одного из образцов. Аналогичная схема используется и при определении теплофизических свойств других материалов.
Рис.6. Теоретическая зависимость безразмерной температуры от безразмерного времени для случая импульсного теплового источника.
МЕТОД ИМПУЛЬСНОГО ПЛОСКОГО ИСТОЧНИКА ТЕПЛА Данный метод определения теплофизических характеристик основывается на решении одномерного уравнения теплопроводности для неограниченного тела в случае действия в нем в течение небольшого промежутка времени t0 плоского источника тепла. Это решение можно получить интегрированием выражения (7.3) по dt в пределах от нуля до t0. Если плоскость действия источника совпадает с плоскостью yz и проходит через точку x 1 = 0, то значение максимума избыточной температуры D T макс = T (x, tмакс) – T 0 на расстоянии x от нагревателя будет соответствовать определенному моменту времени
Если продифференцировать выражение (7.15) по tмакс и приравнять производную d (D T макс)/ d tмакс нулю, получим условие экстремума зависимости избыточной температуры от времени в точке x неограниченного тела, т. е.
Уравнения (7.15) и (7.16) позволяют получить следующие расчетные формулы для теплофизических характеристик:
или
где или
Значения величин j a и j¢l в зависимости от параметра j0 = t0/tмакс приведены в Приложении. Для измерения коэффициента температуропроводности импульсным методом между блоками располагаются две пластины из исследуемого материала, между которыми помещается тонкая пластинка из того же материала. В центре системы располагается источник тепла, включаемый на непродолжительное время (длительность теплового импульса и мощность подбираются экспериментально таким образом, чтобы получился график, подобный рис. 6). Коэффициенты тепло- и температуропроводности рассчитывают по формулам (7.17) и (7.20).
Рис. 7. Схема измерительной ячейки.
|

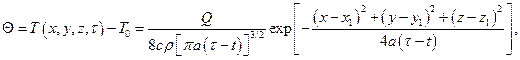 (7.1)
(7.1) (7.2)
(7.2)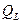 — количество тепла, мгновенно выделяемого единицей длины линейного источника тепла в момент времени t = t.
— количество тепла, мгновенно выделяемого единицей длины линейного источника тепла в момент времени t = t.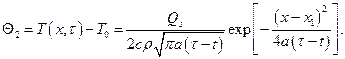 (7.3)
(7.3)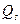 — количество тепла, мгновенно выделяемое единицей площади плоского источника тепла в момент времени t = t.
— количество тепла, мгновенно выделяемое единицей площади плоского источника тепла в момент времени t = t.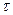 o (в формуле (7.1)
o (в формуле (7.1)  в пределах от 0 до
в пределах от 0 до 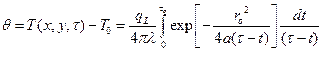 (7.4)
(7.4)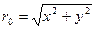 ;
; 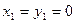 .
.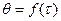 на экстремум, если эта зависимость является результатом кратковременного (импульсного) теплового воздействия.
на экстремум, если эта зависимость является результатом кратковременного (импульсного) теплового воздействия. в точке
в точке 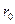 будет соответствовать определённому моменту времени
будет соответствовать определённому моменту времени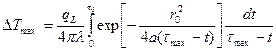 . (7.5)
. (7.5)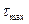 и приравнять производную нулю, то получим соотношение, при котором должно выполняться условие экстремума:
и приравнять производную нулю, то получим соотношение, при котором должно выполняться условие экстремума: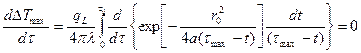 (7.6)
(7.6)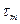 ).
).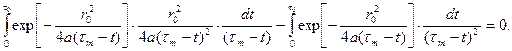 (7.7)
(7.7)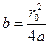 и сделаем замену:
и сделаем замену: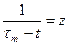 ;
; 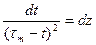 .
.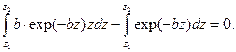 (7.8)
(7.8)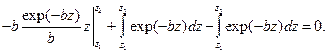
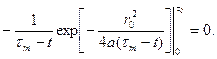
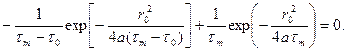
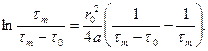 (7.9)
(7.9)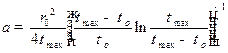
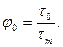 (7.10)
(7.10)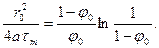 (7.11)
(7.11)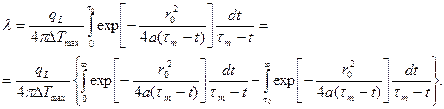
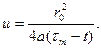
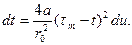
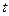 изменяется в пределах от
изменяется в пределах от  до
до 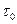 , то новые пределы интегрирования будут:
, то новые пределы интегрирования будут:
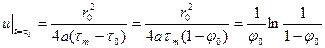

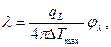 (7.12)
(7.12)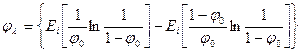 .
.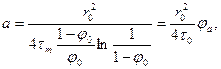 (7.13)
(7.13)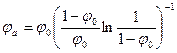 .
.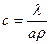 , (7.14)
, (7.14) — плотность образца.
— плотность образца. и
и 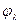 приведены в таблицах.
приведены в таблицах. .
.
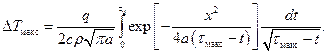 (7.15)
(7.15) (7.16)
(7.16)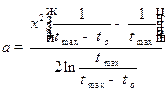 (7.17)
(7.17)
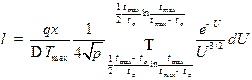 (7.18)
(7.18) (7.19)
(7.19) (7.20)
(7.20)



