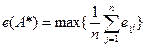V. Критерий Лапласа.
Данный критерий применяется, если состояния внешней среды неизвестны, но их можно считать равновероятными, т. е.
Решающее правило в этом случае имеет следующий вид:
е (A*) = mах{(594+492+240+188) / 4; (554+422+300+238) / 4; (639+452+260+158) / 4} = =mах {378,5; 378,5; 377,25} = 362,5. Следовательно, с точки зрения критерия Лапласа можно выбрать как рынок A1, так и рынок A2.
Методы планирования в условиях риска
I. Принцип Байеса. Если задать вероятности p1=0,3; p2=0,4; р3=0,1; р4=0,2, то получим: e1 = 594 х 0,3+492 х 0,4 + 240 х 0,1 + 188 х 0,2 = 178,2+196,8+24+37,6=436,60; e2 = 554 х 0,3+422 х 0,4+ 300 х 0,1 + 238 х 0,2 = 412,6; e3 = 639 х 0,3+452 х 0,4 + 260 х 0,1 + 158 х 0,2 = 430,1; max{435,411,428,5}=435 (для i=1). Следовательно, оптимальной является альтернатива A1.
Используя матрицу потенциальных потерь, вычислим с учетом вероятностей наступления тех или иных состояний среды общие потери: w1= 0,3 х 45 + 0 + 0,1 х 60 + 0,2 х 50 = 29,5; w2= 0,3 х 85 + 0,4 х 70 + 0 + 0 = 53,5; w3= 0+0,4 х 40 + 0,1 х 40 + 0,2 х 80 = 36. min { w1, w2, w3) = min {29,5; 53,5; 36}= 29,5 (для i=1). Оптимальной альтернативой является A1.
|