Находят область допустимых решений.
Фигура, которая образовалась в результате пересечения всех заштрихованных полуплоскостей, является областью допустимых решений (ОДР). Если хотя бы одна заштрихованная полуплоскость не имеет ни одной общей точки с остальными, то такая система неравенств будет несовместной, а ЗЛП не будет иметь решения.
—•—Ткань ◊;Трудоемкость ̱ ̱ ̱ ̱ ̱;Накладные расходы ̶ ̶;Спрос —*— —•— ―;ЦФ ―;○― ТО Рис. 1 Пересечением всех заштрихованных полуплоскостей на рис. 1 является выпуклый многоугольник ABCDE. Это и есть искомая область допустимых решений. Ход выполнения 1. В поле EXCEL заносим расширенную матрицу ЗЛП (табл. 3). Каждый коэффициент расширенной матрицы заносится в числовом формате в отдельную ячейку. Условия неотрицательности переменных Необходимо достаточно точно и понятно сделать подписи каждого ограничения и каждой переменной. Расширенную матрицу удобно представить в виде табл. 3. Ячейки, содержащие длинные названия и предложения, должны быть отформатированы. Подлежащие форматированию ячейки выделяют черным цветом удержанием левой кнопкой мыши, затем последовательно выполняют следующие действия: в меню EXCEL «Формат» выбирают «Ячейки», находят закладку «Выравнивание», ставят флажок напротив «переносить по словам». В отформатированных таким способом ячейках «длинный» текст будет переноситься на следующую строку таблицы так, как в ячейке А4(табл. 3).
2. Рассчитывают координаты точек пересечения с осями ОХ1 и ОХ2. Каждая прямая имеет две точки пересечения с осями координат: одну с осью ОХ1 и одну с осью ОХ2. Соответственно у каждой точки имеется две координаты. Поскольку имеется две точки пересечения, го всего координат должно быть четыре. Для построения прямой в графическом редакторе EXEL расположите в соседних ячейках одноименные координаты точек пересечения с осями OXI иОХ2.Справа от построенной расширенной матрицы выделите по два столбца с одноименными координатами (табл. 4). В столбцах Е и G табл. 4 будут рассчитываться координаты точки пересечения прямой с осью ОХ2, а в столбцах Fи Н - координаты точки пересечения прямой с осью ОХ1. Для создания шапки при необходимости используйте объединение ячеек. Используйте опцию «Выравнивание» для того, чтобы отрегулировать расположение надписей в табл. 4. Таблица 4
Рассчитайте с помощью формул координаты пересечения первой прямой с осями ОХ1 и ОХ2. Запишите формулы в ненулевые ячейки, предназначенныедля расчета координат. Затем с помощью копирования размножьте формулы по остальным ячейкам. При размножении формул недоступными для операций в EXCEL останутся ячейки, содержащие значение #ДЕЛ/0!. Деление на ноль встречается при расчете координат для прямых, параллельных осям координат. Для построения таких прямых в графиках EXCEL существует два способа: вручную мышкой «растянуть» прямую в нужное положение или ввести в ячейку любое числовое значение, как в ячейке G6 (табл.4). В первом случае необходимо щелкнуть мышкой по построенной прямой. Напрямой появятся маркеры. Вторым щелчком мышки необходимо зацепить нужный маркер и «растянуть» прямую. Сформированные таким способом данные могут быть использованы для построения области допустимых решений. 3. По сформированным данным строят график ОДР в диаграмме EXCEL. На первом шаге построения открывают диаграмму EXCEL и выбирают из всех видов диаграмм «Точечную»,а именно, одну из трех представленных в примере точечных диаграмм с соединительными линиями между точками. На втором шаге построения удаляют из окна «Диапазон» (закладка «Диапазон данных») все автоматически набранные EXCEL диапазоны. В закладке «Ряды» нажимают кнопку «Добавить». В появившемся окне «Имя» с помощью ссылки устанавливают адрес ячейки с названием первого ограничения (табл.5). В окне «Значения X» с помощью ссылки устанавливают адреса ячеек с координатами, которые лежат на оси ОХ1. В окне «Значения У» с помощью ссылки устанавливают значения ячеек с координатами ОХ2. Для создания ссылки достаточно сначала щелкнуть мышкой по диалоговому окну, затем по нужной ячейке поля EXCEL. Таблица 5
На третьем шаге построения диаграммы указывают название диаграммы и подписывают оси 0X1 и 0X2, размечают основные и промежуточные линии сетки и указывают место размещения легенды. Четвертый шаг завершает построение диаграммы - определяют место размещения диаграммы. Это может быть как рабочий лист EXCEL, так и новый. На этом построение ОДР в графическом редакторе EXCEL завершается.
|


 также должны быть представлены в расширенной матрице.
также должны быть представлены в расширенной матрице.

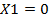
 )
)



